Cho x 8 = y 7 = z 12 và x + y + z = -108. Số lớn nhất trong ba số x; y; z là
A. 27
B. -27
C. -18
D. -45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
TQ
2
CM
1 tháng 3 2017
Ta có: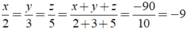 
Khi đó ta có: x = -18 ; y = -27 ; z = -45
Số lớn nhất là -18
Chọn đáp án C.
AH
Akai Haruma
Giáo viên
22 tháng 5 2021
Lời giải:
$x+y+z>\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$
$\Leftrightarrow x+y+z>xy+yz+xz$ (do $xyz=1$)
$\Leftrightarrow x+y+z-xy-yz-xz>0$
$\Leftrightarrow xyz+x+y+z-xy-yz-xz-1>0$
$\Leftrightarrow (x-xy)+(y+z-yz-1)+(xyz-xz)>0$
$\Leftrightarrow x(1-y)+(1-y)(z-1)-xz(1-y)>0$
$\Leftrightarrow (1-y)(x+z-1-xz)>0$
$\Leftrightarrow (1-y)(1-z)(x-1)>0$
$\Leftrightarrow (1-y)(1-z)(1-x)<0(*)$
Nếu trong 3 số $x,y,z$ đều nhỏ hơn $1$ thì $(1-y)(1-z)(1-x)>0$ (mâu thuẫn với $(*)$)
Do đó trong 3 số có ít nhất 1 số lớn hơn $1$.
NT
0
25 tháng 2 2020
Vai trò \(x,y,z\)như nhau không mất tính tổng quát ta giả sử \(x\ge y\ge z\)
Nếu \(x< 2\)thì \(xyz< 2\cdot2\cdot z=4z=z+3z< 2+3z\le2+x+y+z\)(mâu thuẫn)
Vậy \(x\ge2\)
Nếu \(z>2\)thì \(xyz>x\cdot2\cdot2=4x=x+3x>2+3x\ge2+x+y+z\)(mâu thuẫn)
Vậy \(z\le2\)
Nghĩa là có ít nhất 1 số không nhỏ hơn 2 và ít nhất 1 số không lớn hơn 2
