Từ các chữ số 1, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số khác nhau và số tự nhiên đó chia hết cho 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 9 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Gọi số cần lập có dạng a b c ¯ .
Từ a b c ¯ ⋮ 5 ⇒ c = 5 , ta có a b 5 ¯ . Từ a b 5 ¯ ⋮ 3 ⇒ a + b + 5 ⋮ 3 suy ra tồn tại những cặp a ; b là 1 ; 3 ; 1 ; 6 ; 3 ; 4 ; 4 ; 6 Hơn nữa, a và b bình đẳng nên có tổng cộng: 4.2=8 số tìm được. |
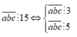
Sơ đồ con đường
Lời giải chi tiết
Gọi số có 3 chữ số chia hết cho 3 là a b c - .
Khi đó tổng các chữ số là a+b+c chia hết cho 3.
Các bộ 3 số thoã mãn điều kiện đó là: 1 ; 3 ; 5 , 1 ; 5 ; 6 , 3 ; 4 ; 5 , 4 ; 5 ; 6
Mỗi bộ 3 lại có:
3 cách chọn hàng trăm.
2 cách chọn hàng chục.
1 cách chọn hàng đơn vị.
Có: 3.2.1= 6 cách chọn.
Vậy tổng có: 4.6= 24 cách chọn.