Tìm tất cả các giá trị của x thỏa mãn x = 1 2
A. x = 0
B. x = ± 1 2
C. x = 1 2
D. x = - 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
LT
1
AD
0
16 tháng 6 2020
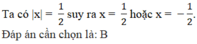
1. Ta có: \(x^2-2xy-x+y+3=0\)
<=> \(x^2-2xy-2.x.\frac{1}{2}+2.y.\frac{1}{2}+\frac{1}{4}+y^2-y^2-\frac{1}{4}+3=0\)
<=> \(\left(x-y-\frac{1}{2}\right)^2-y^2=-\frac{11}{4}\)
<=> \(\left(x-2y-\frac{1}{2}\right)\left(x-\frac{1}{2}\right)=-\frac{11}{4}\)
<=> \(\left(2x-4y-1\right)\left(2x-1\right)=-11\)
Th1: \(\hept{\begin{cases}2x-4y-1=11\\2x-1=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-3\end{cases}}\)
Th2: \(\hept{\begin{cases}2x-4y-1=-11\\2x-1=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=3\end{cases}}\)
Th3: \(\hept{\begin{cases}2x-4y-1=1\\2x-1=-11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=-3\end{cases}}\)
Th4: \(\hept{\begin{cases}2x-4y-1=-1\\2x-1=11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\)
Kết luận:...
7 tháng 2 2022
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-4\right)\\x_1x_2=-m^2+4\end{matrix}\right.\)
\(\dfrac{x_1+x_2}{x_1x_2}+\dfrac{4}{x_1x_2}=1\)
Thay vào ta được : \(\dfrac{2\left(m-4\right)+4}{-m^2+4}=1\Leftrightarrow\dfrac{2m-4}{\left(2-m\right)\left(m+2\right)}=1\Leftrightarrow\dfrac{-2}{m+2}=1\Rightarrow-2=m+2\Leftrightarrow m=-4\)
J
14 tháng 3 2020
a, x + 2 chia hết cho x^2 - 7
=> (x + 2)(x - 2) chia hết cho x^2 - 7
=> x^2 - 4 chia hết cho x^2 - 7
=> x^2 - 7 + 3 chia hết cho x^2 - 7
=> 3 chia hết cho x^2 - 7
=> x^2 - 7 thuộc Ư(3)
=> x^2 - 7 thuộc {-1; 1; -3; 3}
=> x^2 thuộc {6; 8; 4; 10}
mà x là số nguyên
=> x = 2 hoặc x = -2
14 tháng 5 2020
\(A=\left(\frac{2X-1}{x^2-4}+\frac{x+2}{x^2-x-2}\right):\frac{x-2}{x^2+3x+2}ĐK:x\ne\left\{2,-2,-1\right\}\)
a) \(A=\left[\frac{\left(2x-1\right)}{\left(x-2\right)\left(x+2\right)}+\frac{x+2}{\left(x+1\right)\left(x-2\right)}\right]:\frac{x-2}{\left(x+2\right)\left(x+1\right)}\)
\(A=\left[\frac{\left(2x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}\frac{\left(x+2\right)\left(x+2\right)}{\left(x+1\right)\left(x-2\right)\left(x+2\right)}\right].\frac{\left(x+2\right)\left(x+1\right)}{x-2}\)
\(A=\frac{2x^2+x-1+x^2+4x.4}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}.\frac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)}\)
\(A=\frac{3x^2+5x+3}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}.\frac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)}\)
\(A=\frac{3x^2+5x+3}{\left(x-2\right)^2}\)
Ta có :\(3x^2+5x+3\)
\(=3\left(x^2+\frac{5}{3}x+1\right)\)
\(=3\left[x^2+2.\frac{5}{6}x+\frac{25}{36}+\frac{9}{36}\right]\)
\(=3\left[\left(x+\frac{5}{6}\right)^2+\frac{9}{36}\right]>0\)
Mà \(\left(x-2\right)^2>0\)
\(\Rightarrow A>0\left(dpcm\right)\)
\(b,A=11\Leftrightarrow\frac{3x^2+5x+3}{\left(x-2\right)^2}=11\)
\(\Rightarrow3x^2+5x+3=11.\left(x-2\right)^2\)
\(\Rightarrow3x^2+5x+3=11.\left(x^2-4x+4\right)\)
\(\Rightarrow8x^2-49x+41=0\)
\(\Rightarrow8x^2-8x-41x+41=0\)
\(\Rightarrow8x\left(x-1\right)-41\left(x-1\right)=0\)
\(\Rightarrow\left(8x-41\right)\left(x-1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}8x-41=0\\x-1=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{41}{8}\\x=1\end{cases}}}\)(Thỏa mãn)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
\(\Delta=\left(m-1\right)^2-4\left(m+3\right)=m^2-6m-11>0\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=m+3\end{matrix}\right.\)
Ta có:
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m-1\right)^2-2\left(m+3\right)=m^2-4m-5\)
Biểu thức này ko tồn tại cả min lẫn max với điều kiện m từ (1)
