Viết các số tự nhiên có 4 chữ số được lập nên từ chữ số 0 và 1 mà trong đó mỗi chữ số xuất hiện hai lần
A. 1100, 0110, 0101.
B. 1001, 1010, 1100.
C. 0011, 1100, 0101.
D. 1110, 0110, 1001.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Viết các số tự nhiên có 5 chữ số lập nên từ hai chữ số 0 ; 1 mà trong đó chữ số 1 được có mặt ba lần
2
HP
20 tháng 11 2021
Số tự nhiên có 8 chữ số \(\overline{abcdefgh}\).
TH1: \(h=0\)
\(\overline{abcdefg}\) có \(\dfrac{7!}{2!.3!}=420\) cách lập.
\(\Rightarrow\) Lập được 420 số thỏa mãn yêu cầu.
TH2: \(h=5\)
\(\overline{abcdefg}\) có \(\dfrac{7!}{2!.3!}-\dfrac{6!}{2!.3!}=360\) cách lập.
\(\Rightarrow\) Lập được 360 số thỏa mãn yêu cầu.
Vậy lập được \(420+360=780\) số tự nhiên thỏa mãn yêu cầu bài toán.
MA
20 tháng 11 2021
Bạn có thể giải thích phần công thức được không vậy. Mình hiểu hơi chậm. Bạn thông cảm. Mình cảm ơn nhiều.
CM
18 tháng 8 2017
Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: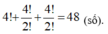 
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: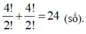 
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: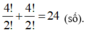 
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: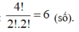 
Vậy có thể lập được 102 số thỏa mãn đề bài.
CM
29 tháng 4 2019
Chọn A
Cách 1:
Ta có S là tập hợp các số tự nhiên gồm 9 chữ số được lập từ X = {6;7;8}, trong đó chữ số 6 xuất hiện 2 lần; chữ số 7 xuất hiện 3 lần; chữ số 8 xuất hiện 4 lần nên
Có cách xếp 2 chữ số 6 vào 2 trong 9 vị trí
Có cách xếp 3 chữ số 7 vào 3 trong 7 vị trí còn lại
Có 1 cách xếp 4 chữ số 8 vào 4 trong 4 vị trí còn lại
Chọn ngẫu nhiên một số từ tập S nên 
Gọi A là biến cố “số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
TH1: 2 chữ số 6 đứng liền nhau
Có 8 cách xếp cho số .Trong mỗi cách như vậy có C 7 3 cách xếp chữ số 7 và 1 cách xếp cho các chữ số 8
Vậy có số 8. C 7 3 .1 = 280 số
TH2: Giữa hai số 6 có đúng 1 chữ số và số đó là số 8.
Có 7 cách xếp cho số .Trong mỗi cách như vậy có C 6 3 cách xếp chữ số 7 và 1 cách xếp các chữ số 8
Vậy có 7. C 6 3 = 140 số
TH3: Giữa hai số 6 có đúng 2 chữ số và đó là hai chữ số 8.
Tương tự Có 6. C 5 3 = 60 số
TH4: Giữa hai số 6 có đúng 3 chữ số và đó là ba chữ số 8.
Có 5. C 4 3 = 20 số
TH5: Giữa hai số 6 có đúng 4 chữ số và đó là bốn chữ số 8.
Có 4. C 4 3 = 4 số
Từ đó suy ra 
Xác suất cần tìm là 
Cách 2:
- Số phần tử không gian mẫu 
- Tính số phần tử của biến cố A“số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
Xếp 2 số 6 có 1 cách: 
Xếp 3 số 7 vào 2 khoảng 
cách ( số cách xếp bằng số nghiệm nguyên không âm của phương trình 
Xác suất cần tìm là 
19 tháng 10 2015
Câu 1:Số phần tử của tập hợp A = {4; 6; 8; ...; 78; 80} là 39
Câu 2:Tìm một số có hai chữ số biết rằng khi viết thêm chữ số 0 vào giữa hai chữ số của số đó thì được số mới gấp 7 lần số đã cho.Số cần tìm là 15
Câu 3:Số phần tử của tập hợp các số tự nhiên chẵn lớn hơn 3 và nhỏ hơn 2000 là 998
Câu 4:Số phần tử của tập hợp các số tự nhiên lẻ lớn hơn 30 và nhỏ hơn 2000 là 998
Câu 5:Số chữ số để đánh số các trang sách (bắt đầu từ trang 1) của một cuốn sách có 1032 trang là 3021
Câu 6:Cho bốn chữ số 1; 9; 7; 8. Có thể lập được bao nhiêu số có hai chữ số khác nhau từ các chữ số trên ? Trả lời:12 số.
Câu 7:Số phần tử của tập hợp các số tự nhiên lẻ lớn hơn 1001 nhưng không vượt quá 2009 là 504
Câu 8:Khi viết liền nhau các số tự nhiên từ 1 đến 99 thì chữ số 5 xuất hiện 20 lần.
Câu 9:Cho bốn chữ số 2; 5; 0; 6. Có thể lập được bao nhiêu số có hai chữ số khác nhau từ các chữ số trên ? Trả lời: 9 số.
Câu 10:Trong ngày hội khỏe Phù Đổng, một trường có 12 học sinh giành được giải thưởng, trong đó có 7 học sinh giành được ít nhất hai giải, 4 học sinh giành được ít nhất ba giải, 2 học sinh giành được số giải nhiều nhất là bốn giải. Hỏi trường đó giành được tất cả bao nhiêu giải ?25 gải
**** mệt quá
16 tháng 9 2015
Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563
Giả sử số cần tìm là abcd
Ta thực hiện các bước sau:
Số cần tìm là số tự nhiên nên a ≠ 0 suy ra a = 1. Như vậy ta còn chữ số 1 và hai chữ số 0 để xếp vào 3 vị trí còn lại
Nếu xếp chữ số 0 vào vị trí b thì ta được số cần tìm là 1001 hoặc1010
Nếu xếp chữ số 1 vào vị trí b thì ta được số cần tìm là 1100Vậy ta có ba số cần tìm là 1001; 1010; 1100
Đáp án B