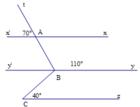
Cho hình vẽ bên. Chứng minh:
a) Ax // By
b) By // Cz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 9 2021
\(a,\widehat{xAB}+\widehat{xAt}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAB}=180^0-60^0=120^0\\ \Rightarrow\widehat{xAB}=\widehat{yBA}\left(=120^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(Ax//By\)
\(b,\widehat{yBC}+\widehat{ABC}+\widehat{yBA}=360^0\\ \Rightarrow\widehat{yBC}=360^0-120^0-90^0=150^0\\ \Rightarrow\widehat{yBC}=\widehat{BCz}\left(=150^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(By//Cz\)
PT
1
CM
29 tháng 7 2018
a) Ta có x'At ^ + tAx ^ = 180 ∘ (hai góc kề bù)
mà x'At ^ = 70 ∘
⇒ xAt ^ = 180 ∘ − 70 ∘ = 110 ∘
Mặt khác ABy ^ = 110 ∘
⇒ xAt ^ = ABy ^ mà hai góc này ở vị trí đồng vị
⇒ By // xx'
b)
Kẻ tia By' là tia đối của tia By
Vì By // xx' nên By' // xx'
⇒ x'At ^ = ABy' ^ = 70 ∘ (hai góc đồng vị)
Mặt khác ABC ^ = ABy' ^ + y'BC ^
Mà ABC ^ = 110 ∘ và ABy' ^ = 70 ∘
⇒ y'BC ^ = 110 ∘ − 70 ∘ = 40 ∘
Ta lại có BCz ^ = 40 ∘
⇒ y'BC ^ = BCz ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz