Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính đọ dài cạnh còn lại của tứ giác ABCD.
A. BC = 6cm
B. BC = 4cm
C. BC = 5cm
D. BC = 3cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

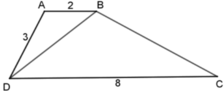
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D

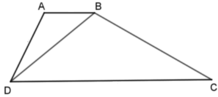
Vì ΔABD ⁓ ΔBDC (gt) nên A B D ^ = B D C ^ (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB // CD suy ra ABCD là hình thang (dấu hiệu nhận biết) hay B đúng
Lại có ΔABD ⁓ ΔBDC nên A B B D = A D B C (cạnh tương ứng) nên A đúng
ΔABD ⁓ ΔBDC => A B B D = B D D C (cạnh tương ứng)
=> AB.CD = B D 2 hay C đúng
Chỉ có D sai
Đáp án: D

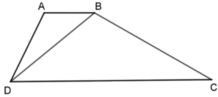
Vì ΔABD ⁓ ΔBDC (gt) nên A B D ^ = B D C ^ (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB // CD suy ra ABCD là hình thang (dấu hiệu nhận biết)
Đáp án: D

a: Xét ΔABD và ΔBDC có
AB/BD=BD/DC=AD/BC
Do đó: ΔABD∼ΔBDC
b: Ta có: ΔABD=ΔBDC
nên \(\widehat{ABD}=\widehat{BDC}\)
hay AB//CD
=>ABCD là hình thang

a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 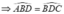 Þ ĐPCM
Þ ĐPCM

a: Xét ΔABD và ΔBDC có
AB/BD=BD/CD=AD/BC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng với ΔBDC
=>góc ABD=góc BDC
=>AB//CD

Bài làm
a) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\widehat{ABD}=\widehat{BDC}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AB // CD
b) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\frac{AB}{CD}=\frac{AD}{BC}=\frac{BD}{BD}\)
hay \(\frac{2}{8}=\frac{3}{BC}=\frac{BD}{BD}\)
=> BC = 8 . 3 : 2 = 12 ( cm )
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: A