Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Biết D và M lần lượt là giao điểm của AI, AG với BC. Chọn khẳng định sai:
A. IG // BC
B. A I I D = A G G M
C. A B G ^ = C B G ^
D. I D A D = M G M A

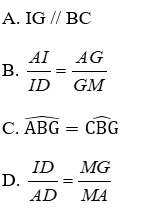

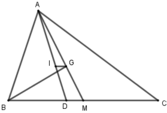
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C