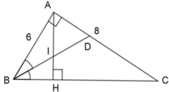
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn khẳng định đúng.
A. AB.BI = BD.HB
B. A B . B I = A I 2
C. A B . B I = B D 2
D. A B . B I = H I 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\)(Định lí tia phân giác của tam giác)
\(\Leftrightarrow\dfrac{AD}{6}=\dfrac{DC}{10}\)
mà AD+DC=AC(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{DC}{10}=\dfrac{AD+DC}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{DC}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\DC=5\left(cm\right)\end{matrix}\right.\)
Vậy: AD=3cm; DC=5cm
2 tháng 4 2021
b) Xét ΔABH có BI là đường phân giác ứng với cạnh AH(Gt)
nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\)(Tính chất đường phân giác của tam giác)(1)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}\)(Tính chất đường phân giác của tam giác)(2)
Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH∼ΔCBA(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)(đpcm)
TH
9 tháng 3 2022
Dành cho anh em nào cần phần C nha
Xét ∆HIB và ∆AID có:
Góc IHB= góc IAD
Góc I( đối đỉnh)
Suy ra ∆HIB đồng dạng vs ∆ AID
Suy ra góc HBI = ADI
Mà tâm giác BIH vuông tại H nên Góc HBI = BIH
Mà hai góc I đối đỉnh nên góc HBI = AID
Mà góc HBI = ADI
Nên góc ADI = góc AID
Suy ra tâm giác AID cân (đpcm) (hơi dài nhỉ nhưng có cách ngắn nhưng nó sẽ không chi tiết mong ae thông cảm )
21 tháng 3 2021
a, Xét tam giác ABC vuông tại A, có AH là đường cao
Áp dụng định lí Py ta go ta có :
\(BC^2=AB^2+AC^2=36+64\)
\(\Rightarrow BC^2=100\Rightarrow BC=10\)cm
Vì BD là phân giác ^ABC nên
\(\frac{AB}{BC}=\frac{AD}{DC}\)(1) mà \(AD=AC-DC=8-DC\)
hay \(\frac{6}{10}=\frac{8-DC}{DC}\Rightarrow6DC=80-10DC\)
\(\Leftrightarrow16DC=80\Leftrightarrow DC=5\)cm
\(\Rightarrow AD=AC-DC=8-5=3\)cm
b, Xét tam giác BHA và tam giác BAC ta có
^BHA = ^A = 900
^B _ chung
Vậy tam giác BHA ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{BH}{BA}=\frac{AB}{BC}\) ( tỉ số đồng dạng ) (2)
Từ (1) và (2) \(\Rightarrow\frac{BH}{BA}=\frac{AD}{DC}\)(3)
xem lại đề đi nếu như thành \(\frac{IH}{AD}=\frac{IA}{DC}\)
sao lại có tam giác IHA được ? hay còn cách nào khác ko ?
CM
11 tháng 1 2019
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 6 2 + 8 2 = B C 2 ⇔ B C 2 = 100 ⇒ B C = 10 c m
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
B A A D = B C C D ⇔ B A A D = B C C A − A D ⇔ 6 A D = 10 8 − A D
=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm
Đáp án: B
MN
12 tháng 5 2018
a) Xét \(\Delta BAH\) và \(\Delta BCA\)có:
\(\widehat{B}\) chung
\(\widehat{BHA}=\widehat{BAC}=90^0\)
suy ra: \(\Delta BAH~\Delta BCA\) (g.g)
\(\Rightarrow\)\(\frac{AB}{BC}=\frac{BH}{AB}\)
\(\Rightarrow\)\(AB^2=BH.BC\)
c) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\)\(BC=10\)
\(\Delta ABC\)có AK là phân giác
\(\Rightarrow\)\(\frac{KB}{AB}=\frac{KC}{AC}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{KB}{AB}=\frac{KC}{AC}=\frac{KB+KC}{AB+AC}=\frac{5}{7}\)
suy ra: \(KB=\frac{30}{7}\) \(KC=\frac{40}{7}\)
c) Xét \(\Delta ABD\)và \(\Delta HBI\)có:
\(\widehat{ABD}=\widehat{HBI}\) (gt)
\(\widehat{BAD}=\widehat{BHI}=90^0\)
suy ra: \(\Delta ABD~\Delta HBI\)
\(\Rightarrow\)\(\frac{AB}{HB}=\frac{BD}{BI}\)
\(\Rightarrow\)\(AB.BI=BD.HB\)
d) \(S_{ABC}=\frac{1}{2}.AB.AC=24\)
\(\Delta ABH~\Delta CBA\) (câu a)
\(\Rightarrow\)\(\frac{S_{ABH}}{S_{CBA}}=\left(\frac{AB}{BC}\right)^2=\frac{9}{16}\)
\(\Rightarrow\)\(S_{ABH}=\frac{9}{16}.S_{ABC}=13,5\)
VP
12 tháng 5 2018
â) chứng minh AB2 = BH . BC
Xét : \(\Delta ABHva\Delta ABC,co\):
\(\widehat{B}\) là góc chung
\(\widehat{A}=\widehat{H}=90^o\)
Do do : \(\Delta ABH~\Delta ABC\left(g-g\right)\)
=> \(\frac{AB}{HB}=\frac{BC}{AB}\) (tỉ lệ tương ứng của 2 tam giác đồng dạng )
=> AB . AB = BH . BC
=> AB2 = BH . BC
b)
9 tháng 5 2023
a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔBAC có BD là phan giác
=>AD/AB=DC/BC
=>AD/3=DC/5=8/8=1
=>AD=3cm; DC=5cm
b: Xét ΔBAD vuông tại A va ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>AD/HI=BA/BH
=>AD*BH=HI*BA
c: góc ADI=góc BIH=góc AID
=>ΔAID cân tại A
3 tháng 4 2023
a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
góc CBD=góc ABD
=>góc AID=góc ADI
=>ΔAID cân tại A
LD
30 tháng 3 2022
a, Xét ΔABC và ΔHBA có :
\(\widehat{A}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔABC vuông tại A, theo định lý Pi-ta-go ta có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có : \(\Delta ABC\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AC}{AH}=\dfrac{BC}{AB}\)
hay \(\dfrac{8}{AH}=\dfrac{10}{6}\)
\(\Rightarrow AH=\dfrac{8.6}{10}=4,8\left(cm\right)\)
c, Xét ΔAHB và ΔCHA có :
\(\widehat{BHA}=\widehat{AHC}=90^0\)
\(\widehat{BAH}=\widehat{C}\left(phụ\cdot với\cdot\widehat{B}\right)\)
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{BH}{AH}\)
\(\Rightarrow AH^2=HC.BH\)
d, Xét ΔABD và ΔHBI có :
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{ABD}=\widehat{HBI}\left(phân\cdot giác\cdot BD\right)\)
\(\Rightarrow\Delta ABD\sim\Delta HBI\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BD}{BI}\)
\(\Rightarrow AB.BI=BD.HB\left(đpcm\right)\)
Xét 2 tam giác vuông ABD và HBI có:
A B D ^ = H B I ^ (BD là tia phân giác của góc B)
=> ΔABD ~ ΔHBI (g - g)
⇒ A B H B = B D B I ⇔ AB.BI = BD.HB
Đáp án: A