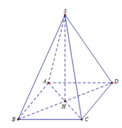
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SB = 5cm. Tính bình phương đường cao SH của hình chóp
A. 41 2
B. 41
C. 82 3
D. 22
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 6 2019
a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
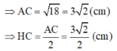
Lại có: SH2 = SC2 - HC2 (Pytago)
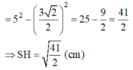
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
CM
23 tháng 4 2018
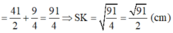
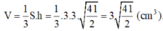
Đáp án B
Ta có: 2 B H 2 = a 3 2 ⇒ B H 2 = 3 a 2 2
S H = S B 2 − B H 2 = 2 a 2 − 3 a 2 2 = a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 . S H . S A B C D = 1 3 . a 2 . a 3 2 = a 3 2
CM
10 tháng 10 2017
Chọn B.
Gọi H là tâm của hình vuông ABCD thì SH ⊥ (ABCD)
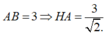
Do đó
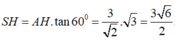
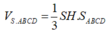
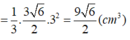
Đáp án cần chọn là: A