Cho tam giác ABC . Các góc A,B,C tỉ lệ lần lượt với 7;5;3 . Các góc ngoài tương ứng tỉ lê với các số nào.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A^o,B^o,C^o\)lần lượt tỉ lệ với 7:7:16
\(\Rightarrow\frac{A^o}{7}=\frac{B^o}{7}=\frac{C^o}{16}\)và \(A^o+B^o+C^o=180^o\)( Tổng 3 góc trong của tam giác )
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{A^o}{7}=\frac{B^o}{7}=\frac{C^o}{16}=\frac{A^o+B^o+C^o}{7+7+16}=\frac{180^o}{30}=6^o\)
=> góc A = 42o , góc B = 42o , góc C = 96o

Answer:
Ta có: Ba góc của tam giác lần lượt tỉ lệ với 1, 2, 3
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}\) và \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+2+3}=30^o\)
\(\Rightarrow\frac{\widehat{A}}{1}=30^o\Rightarrow\widehat{A}=30^o\)
\(\Rightarrow\frac{\widehat{B}}{2}=30^o\Rightarrow\widehat{B}=60^o\)
\(\Rightarrow\frac{\widehat{C}}{3}=30^o\Rightarrow\widehat{C}=90^o\)

theo dãy tỉ số bằng nhau:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{180}{15}=12\)
=> a=12.3=360
=> b=12.5=600
=> c=12.7=840
áp dụng t/c của dãy tỉ số bằng nhau ta được :\(\frac{a}{3}\)= \(\frac{b}{5}\)=\(\frac{c}{7}\)=\(\frac{a+b+c}{3+5+7}\)=\(\frac{180}{15}\)=12
\(\Rightarrow\frac{a}{3}=12\Rightarrow a=12.3=36\)
\(\Rightarrow\frac{b}{5}=12\Rightarrow b=12.5=60\)
\(\Rightarrow\frac{c}{7}=12\Rightarrow c=12.7=84\)

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{180}{12}=15\)
Do đó: a=45; b=60; c=75

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: b=60

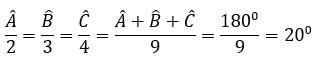
Gọi a,b,c là các góc A,B,C tỉ lệ lần lượt với 7;5;3
a/7=b/5=c/3 va a+b+c=180
Ap dung tinh chat day ti so bang nhau ta co :
a/7=b/5=c/3=a+b+c/7+5+3=180/15=12
Suy ra :a/7=12=>a=12.7=84
b/5=12=>b=12.5=60
c/3=12=>c=12.3=36
****
bạn này giải sai rồi ,các góc ngoài tỉ lệ lần lượt với 4;5;6