so sánh tổng S = (1/2) + (2/2^2) + (3/2^3)+...+(n/2^n)+...+(2019/2^2019) với 2 (n >0 và n nguyên dương )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
N
1

13 tháng 5 2019
\(S=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{n}{2^n}+...+\frac{2007}{2^{2007}}\)
Ta có: \(\frac{n}{2^n}=\frac{n+1}{2^{n-1}}-\frac{n+2}{2^n}\)
\(\Rightarrow\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{2007}{2^{2007}}\)
\(=\frac{1}{2}+\left(\frac{3}{2}-\frac{4}{2^3}\right)+\left(\frac{4}{2^3}-\frac{5}{2^3}\right)+...+\left(\frac{2008}{2^{2006}}-\frac{2009}{2^{2007}}\right)\)
\(=\frac{1}{2}+\frac{3}{4}-\frac{2009}{2^{2007}}\)
\(=2-\frac{2009}{2^{2007}}< 2\)
~ Học tốt ~ K cho mk nhé! Thank you.
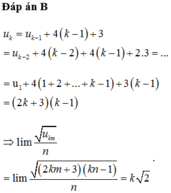
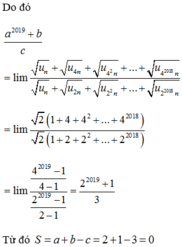
Ta có \(S=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{2018}{2^{2018}}+\frac{2019}{2^{2019}}\)
=> 2S = \(1+1+\frac{3}{2^2}+...+\frac{2018}{2^{2017}}+\frac{2019}{2^{2018}}\)
Khi đó 2S - S = \(\left(1+1+\frac{3}{2^2}+..+\frac{2018}{2^{2017}}+\frac{2019}{2^{2018}}\right)-\left(\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{2018}{2^{2018}}+\frac{2^{2019}}{2019}\right)\)
=> S = \(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2017}}+\frac{1}{2^{2018}}-\frac{2019}{2^{2019}}\)
Đặt P = \(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2017}}+\frac{1}{2^{2018}}\)
=> 2P = \(2+1+\frac{1}{2}+...+\frac{1}{2^{2016}}+\frac{1}{2^{2017}}\)
Khi đó 2P - P = \(\left(2+1+\frac{1}{2}+...+\frac{1}{2^{2016}}+\frac{1}{2^{2017}}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2017}}+\frac{1}{2^{2018}}\right)\)
P = \(2-\frac{1}{2^{2018}}\)
Thay P vào S
=> S = \(2-\frac{1}{2^{2018}}-\frac{2019}{2^{2019}}=2-\frac{2}{2^{2019}}-\frac{2019}{2^{2019}}=2-\frac{2021}{2^{2019}}< 2\)
Vậy S < 2