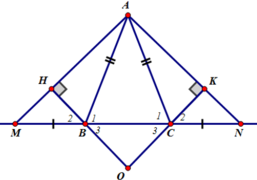
Cho tam giác ABC cân tại A. Trên tia đối của tia BC vẽ điểm M. Trên tia đối của tia CB lấy điểm N sao cho BM=CN. CM: Tam giác AMN là tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Bn tham khảo nhé!
CM
16 tháng 2 2017
ΔABC cân tại A suy ra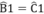 
Ta lại có :
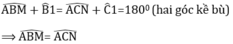
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
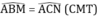
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
HL
27 tháng 2 2015
Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)
9 tháng 1 2022
Xét ΔBAM và ΔCAN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO dó: ΔBAM=ΔCAN
Suy ra: AM=AN
hay ΔAMN cân tại A
CM
14 tháng 9 2017
Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒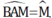 
Mà theo tính chất góc ngoài trong ΔBAM thì
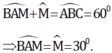
Tương tự ta có
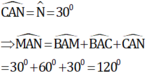
* Ta chứng minh tam giác OBC là tam giác đều.
HT
8 tháng 7 2016
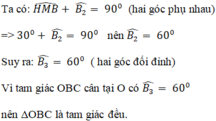
(Bạn tự vẽ hình)
Có tam giác ABC cân tại A
=> AB = AC và góc ABC = góc ACB
=> góc ABM = góc ACN (vì cùng kề bù với 2 góc bằng nhau)
Xét tam giác ABM và tam giác ACN có:
AB = AC (cmt)
góc ABM = goác ACN (cmt)
BM = CN (gt)
=> tam giác ABM = tam giác ACN (c.g.c)
=> AM = AN (2 cạnh tương ứng)
=> tam giác AMN cân tại A (Đpcm)
