Giúp em câu 6 câu 7 câu 9 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
2
26 tháng 10 2021
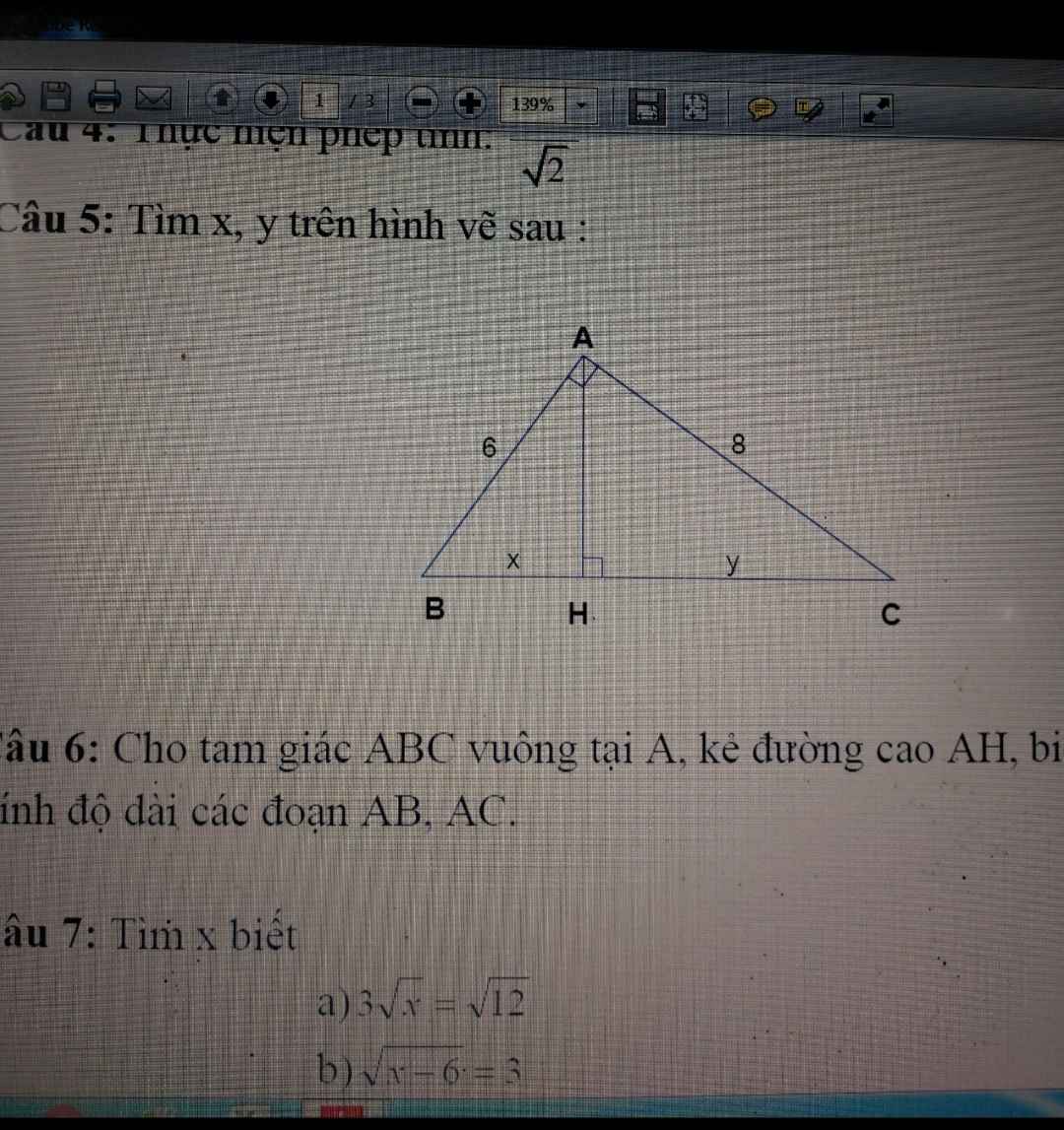
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
14 tháng 5 2023
5:
=10x^3*1/2xy-2/5y*1/2xy+1/2z*1/2xy
=5x^3y-1/5xy^2+1/4xyz
6: =x^2y*4xy+x^2y*3y-5x*x^2y
=4x^3y^2+3x^2y^2-5x^3y
7: =-4/3xy*3x^2y+4/3xy*6xy-4/3xy*9x
=-4x^3y^2+8x^2y^2-12x^2y
giúp em câu 8 câu 9 với em cần gấp ạ
H
22 tháng 7 2021
Câu 9 :
a) $FeO + H_2SO_4 \to FeSO_4 + H_2O$
$n_{FeSO_4} =n_{H_2SO_4} = n_{FeO} = \dfrac{7,2}{72} = 0,1(mol)$
$m_{dd\ H_2SO_4} = \dfrac{0,1.98}{24,5\%} = 40(gam)$
$m_{dd\ sau\ pư} = 40 + 7,2 = 47,2(gam)$
Gọi $n_{FeSO_4.7H_2O} = a(mol)$
Sau khi tách :
$m_{dd} = 47,2 - 278a(gam)$
$n_{FeSO_4} = 0,1 - a(mol)$
Suy ra :
$C\% = \dfrac{152(0,1 - a)}{47,2 - 278a}.100\% = 12,18\%$
$\Rightarrow a = 0,08$
$m = 0,08.278 =22,24(gam)$
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
9.
Gọi D là trung điểm BC \(\Rightarrow AD\perp BC\) (do tam giác ABC đều)
Mặt khác \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAD\right)\)
Mà BC là giao tuyến (SAB) và (SBC)
\(\Rightarrow\widehat{SDA}\) là góc giữa (ABC) và (SBC)
\(AD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow\widehat{SDA}=30^0\)
b.
Câu b nhìn không rõ, đề yêu cầu tính diện tích tam giác SBC đúng không nhỉ?
Từ câu a ta có \(BC\perp\left(SAD\right)\Rightarrow SD\perp BC\)
Pitago tam giác SAD: \(SD=\sqrt{SA^2+AD^2}=a\)
\(\Rightarrow S_{\Delta SBC}=\dfrac{1}{2}SD.BC=\dfrac{a^2}{2}\)
Chụp thế này mà teo tức:(
Mực xanh mực đỏ lại còn mờ