Question

[bùi hương gaing]

: Cho đoạn mạch gồm hai điện trở R₁= 15Ω, R₂= 25Ω được mắc vào hiệu điên thế 25V. Tính điện trở tương đương, cường độ dòng điện trong mạch chính và cường độ dòng điện qua các điện trở thành phần, hiệu điện thế hai đầu mỗi điện trở khi:

a) R₁ nối tiếp với R₂

b) R₁ song song với R_2,

Answer 1

[nthv_.]

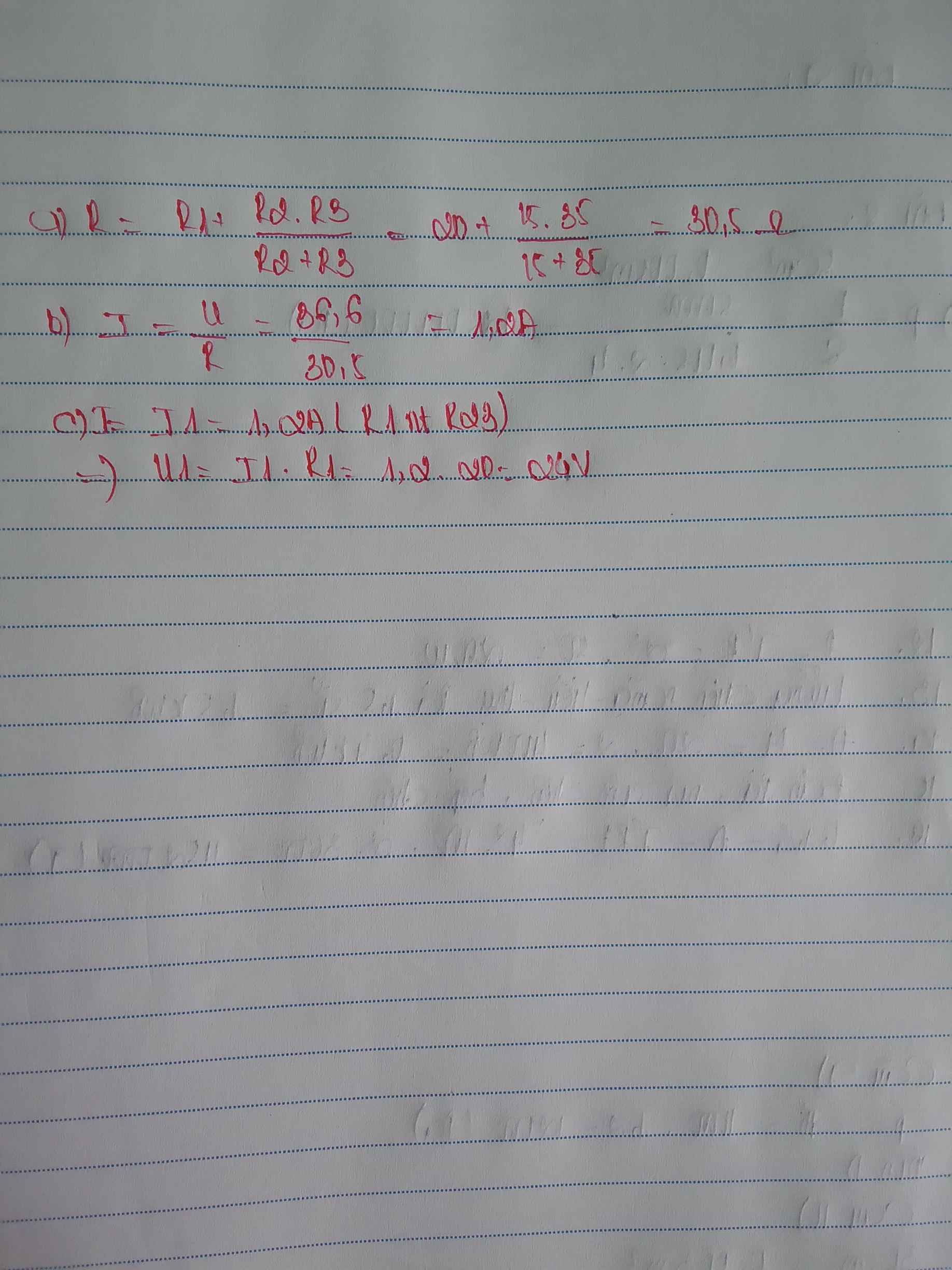
a.

\(R=R1+R2=15+25=40\left(\Omega\right)\)

\(I=I1=I2=U:R=25:40=0,625\left(A\right)\)

\(\left[{}\begin{matrix}U1=I1.R1=0,625.15=9,375\left(V\right)\\U2=I2.R2=0,625.25=15,625\left(V\right)\end{matrix}\right.\)

b. 

\(R=\dfrac{R1.R2}{R1+R2}=\dfrac{15.25}{15+25}=9,375\left(\Omega\right)\)

\(U=U1=U2=25V\)(R1//R2)

\(I=U:R=25:9,375=\dfrac{8}{3}\left(A\right)\)

\(\left[{}\begin{matrix}I1=U1:R1=25:15=\dfrac{5}{3}\left(A\right)\\I2=U2:R2=25:25=1\left(A\right)\end{matrix}\right.\)

Answer 2

[nguyễn thị hương giang]

a) \(R_1ntR_2\)

    \(R_{tđ}=R_1+R_2=15+25=40\Omega\)

    \(I_1=I_2=I_m=\dfrac{25}{40}=0,625A\)

    \(U_1=R_1\cdot I_1=15\cdot0,625=9,375V\)

    \(U_2=R_2\cdot I_2=25\cdot0,625=15,625V\)

b) \(R_1//R_2\)

     \(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{15\cdot25}{15+25}=9,375\Omega\)

     \(U_1=U_2=U_m=25V\)

     \(I_m=\dfrac{25}{9,375}=\dfrac{8}{3}A\)

     \(I_1=\dfrac{U_1}{R_1}=\dfrac{25}{15}=\dfrac{5}{3}A\)

     \(I_2=\dfrac{U_2}{R_2}=\dfrac{25}{25}=1A\)