Cho biết tập hợp tất cả các giá trị của tham số m để phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 2 m + 1 = 0 có nghiệm là S = [ - a b ; + ∞ ) , với a, b là các số nguyên dương và a b là phân số tối giản. Tính T = a + b .
A. T = 13.
B. T = 17.
C. T = 49.
D. T = 3.



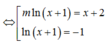
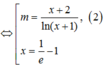

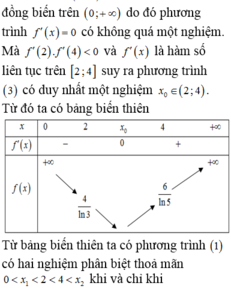
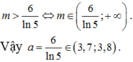

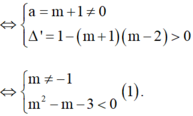
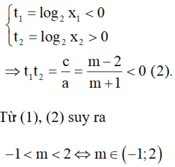
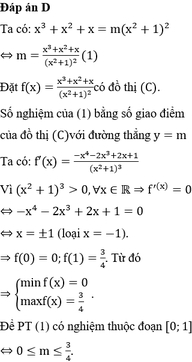
Điều kiện xác định: x ≠ 0 .
Đặt t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2
Phương trình đã cho trở thành 2 t 2 − 2 − 3 t − 2 m + 1 = 0
⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m ( 1 )
Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:
(1) Có nghiệm t thỏa mãn t ≥ 2 t ≤ − 2 k h i 2 m ≥ − 1 2 m ≥ 11 ⇔ m ≥ − 1 2 ⇒ S = − 1 2 ; + ∞
Vậy T = 3
Đáp án cần chọn là: D