Cho hai điểm cố định B, C trên đường tròn (O) và một điểm A thay đổi trên đường tròn đó. Tìm quĩ tích trực tâm H của △ ABC:
A.Là đường tròn (O) bán kính = BC
B. Là đường thẳngđi qua BC và vuông góc với BC tại I ( là trung điểm của BC)
C. Là đường tròn tâm (O’) (ảnh của (O) qua phép tịnh tiến theo vectơ B C → )
D.Là đường tròn tâm (O’) ( ảnh của (O) qua phép tịnh tiến theo vectơ B ' C → với BB’ là đường kính đường tròn (O))


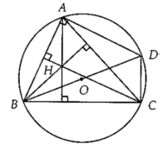
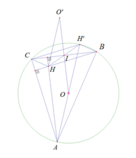
Đáp án D
Gọi BB’ là đường kính (O).
T B ' C → : O → O ' ⇒ O O ' / / B ' C (1)
Ta lại có
B’C // AH ( cùng vuông góc BC) (2)
B’A // CH ( cùng vuông góc BA)
AH = B’C (3)
Từ (1), (2), (3): O O ' / / A H O O ' = A H =>O’H = OA = R
=> H ∈ (O’,R)