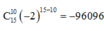Cho n là số nguyên dương thỏa mãn A n 2 - 3 C n n - 1 = 11 n . Xét khai triển P x = x - 2 n . Hệ số chứa x 10 trong khai triển là:
A. 384384
B. - 3075072
C. - 96096
D. 3075072
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C^1_n+C^2_n=15\)
=>\(n+\dfrac{n!}{\left(n-2\right)!\cdot2!}=15\)
=>\(n+\dfrac{n^2-n}{2}=15\)
=>2n+n^2-n=30
=>n^2+n-30=0
=>n=5
=>(x+2/x^4)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(\dfrac{2}{x^4}\right)^k=C^k_5\cdot x^{5-5k}\cdot2^k\)
SỐ hạng ko chứa x tương ứng với 5-5k=0
=>k=1
=>Số hạng đó là 5*2=10

Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
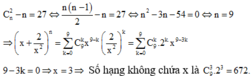
Đáp án C
Phương pháp:
+) Công thức khai triển nhị thức Newton:
+)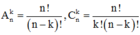
Cách giải:
Với n =15: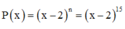
Hệ số chứa x 10 ứng với i = 10 và bằng