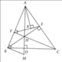
Cho tam giác ABC nhọn. Kẻ các đường cao BE và CF cắt nhau tại H.
1) Chứng minh A E . A C = A F . A B v à Δ A E F ∽ Δ A B C .
2) Qua B kẻ đường thẳng song song với CF cắt tia AH tại M. AH cắt BC tại D. Chứng minh B D 2 = A D . D M .
3) Cho A C B ^ = 45 0 và kẻ AK vuông góc với EF tại K. Tính tỉ số S A F H S A K E .
4) Chứng minh: A B . A C = B E . C F + A E . AF