Cho hình chóp đều S.ABCD. Xét các khẳng định sau:
i) Đáy ABCD là hình vuông;
ii) SA = SB = SC = SD;
iii) Hình chóp có bốn mặt;
iv) SO vuông góc vói mặt đáy, với O là trung điểm AB.
Số khẳng định sai là:
A. 1;
B. 2;
C. 3;
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
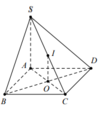
Vì O,I lần lượt là trung điểm của AC,SC. Suy ra OI//SA mà S A ⊥ A B C D ⇒ O I ⊥ A B C D .
S A ⊥ A B C D ⇒ S A ⊥ B D mà B D ⊥ A C ⇒ B D ⊥ S A C .
Ta có S A ⊥ C D A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D ⇒ ∆ S C D vuông tại D.
Suy ra ID = IC tương tự ta được I B = I C ⇒ I A = I B = I C = I D .
BC không vuông góc với mặt phẳng (SCD) vì S C B ^ < 90 °
Vậy có hai khẳng định đúng là 1 và 3.

Chọn D.
Vì S A ⊥ ( A B C D ) nên AC là hình chiếu vuông góc của SC lên(ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
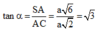
⇒ α = 60 o

Vì S A ⊥ A B C D nên AC là hình chiếu vuông góc của SC lên (ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
tan α = S A A C = a 6 a 2 = 3 ⇒ α = 60 o
Chọn D
Đáp án B