Tam giác ABC cân tại A có góc A =100 độ ,lấy các điểm D và E sao cho trên cạnh BC có BD=BA , CE=CA.Tính góc DAE?
Giải giúp vs MAI NỘP RỒIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
12 tháng 1 2018
Tam giác BAD cân nên ˆBDA=ˆBAD=700BDA^=BAD^=700. Từ đó ˆDAC=300DAC^=300
Tương tự ta tính được ˆBAE=300BAE^=300
Vậy ˆDAE=40
26 tháng 12 2018
ΔABD cân tại B có 
ΔACE cân tại C có 
YN
26 tháng 12 2021
Answer:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{C}+\widehat{B}=180^o\)
\(\Rightarrow2\widehat{B}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\)
Ta có: Tam giác ACE cân tại C
Mà: \(\widehat{A}+\widehat{C}+\widehat{E}=180^o\)
\(\Rightarrow2\widehat{E}+40^o=180^o\)
\(\Rightarrow2\widehat{E}=140^o\)
\(\Rightarrow\widehat{E}=70^o\) (1)
Ta có: Tam giác ABD cân tại B
Mà: \(\widehat{A}+\widehat{B}+\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}+40^o=180^o\)
\(\Rightarrow2\widehat{D}=140^o\)
\(\Rightarrow\widehat{D}=70^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\widehat{E}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{A}+2.70^o=180^o\)
\(\Rightarrow\widehat{A}+140^o=180^o\)
\(\Rightarrow\widehat{A}=40^o\)
Vậy \(\widehat{DAE}=40^o\)
NT
1
26 tháng 12 2018
ΔABD cân tại B có
ΔACE cân tại C có
15 tháng 7 2015
Ta có:
BA = BD => tam giác ABD cân tại B => góc BAD = góc BDA (1)
CE = CA => tam giác ACE cân tại C => góc EAC = góc CEA (2)
....
LH
2
11 tháng 2 2020
Vì \(\Delta ABC\)cân tại \(A\left(gt\right)\)
\(\Rightarrow\widehat{B}=\widehat{C}\)( tính chất tam giác cân )
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-100^0}{2}=\frac{80^0}{2}=40^0\)
Xét \(\Delta ABD\)có:
\(BD=BA\left(gt\right)\)
\(\Rightarrow\Delta ABD\)cân tại B
\(\Rightarrow\widehat{BAD}=\widehat{ADB}\)( tính chất tam giác cân )
\(\Rightarrow\widehat{BAD}=\widehat{ADB}=\frac{180^0-\widehat{B}}{2}\)
\(\Rightarrow\widehat{BAD}=\widehat{ADB}=\frac{180^0-40^0}{2}=\frac{140^0}{2}=70^0\)
\(\Rightarrow\widehat{ADB}=70^0\)
Hay \(\widehat{ADE}=70^0\)
Xét \(\Delta ADE\)có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{AED}=180^0\)( định lý tổng 3 góc trong 1 tam giác )
\(\Rightarrow\widehat{DAE}+70^0+70^0=180^0\)
\(\Rightarrow\widehat{DAE}+140^0=180^0\)
\(\Rightarrow\widehat{DAE}=180^0-140^0\)
\(\Rightarrow\widehat{DAE}=40^0\)
Vậy \(\widehat{DAE}=40^0\)
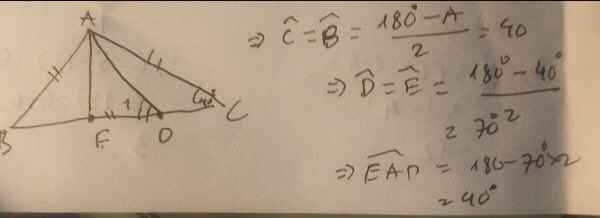
- Đây nè bạn ~> http://olm.vn/hoi-dap/question/130302.html
- Tick cho mềnh nha ^^~