Cho hàm số (P): \(y=f\left(x\right)=x^2+4x+3\).
a. Khảo sát và vẽ đồ thị hàm số.
b. Dựa vào đồ thị tìm x để f(x) > 0, f(x) < 0.
c. Dựa vào đồ thị tìm m để phương trình \(x^2-4x+2-m=0\).
d. Tìm m để (P) cắt (d): y = 2x + m - 5 tại 2 điểm phân biệt.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2021
a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
CM
1 tháng 6 2017
Đáp án B
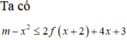
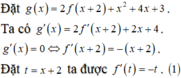
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
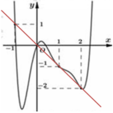
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có
22 tháng 4 2020
Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)
11 tháng 12 2021
a: Thay x=10 và y=-15 vào f(x), ta được:
10m-20=-15
=>10m=5
hay m=1/2
a, Bảng biến thiên:
Đồ thị hàm số:
b, \(f\left(x\right)>0\Leftrightarrow x\in\left(-\infty;-3\right)\cup\left(-1;+\infty\right)\)
\(f\left(x\right)< 0\Leftrightarrow x\in\left(-3;-1\right)\)
c, Yêu cầu bài toán là gì vậy:v
d, Phương trình hoành độ giao điểm của \(\left(P\right);\left(d\right)\):
\(x^2+4x+3=2x+m-5\)
\(\Leftrightarrow x^2+2x+8-m=0\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(\left(1\right)\) có hai nghiệm phân biệt
\(\Delta'=1-\left(8-m\right)=m-7>0\Leftrightarrow m>7\)