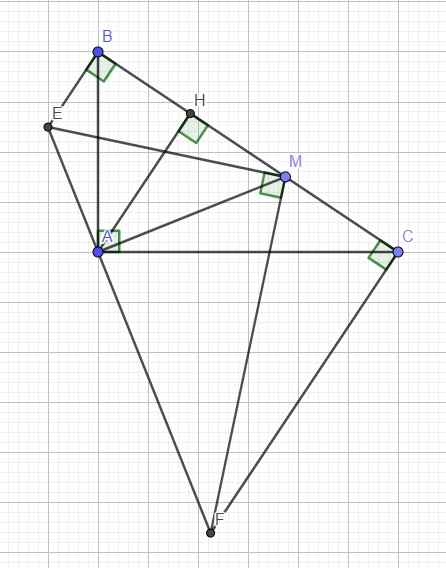
Cho ∆ABC vuông tại A, trung tuyến AM, đường cao AH. Trên cùng mặt phẳng bờ BC, kẻ 2 tia Bx và Cy cùng vuông góc với BC. Qua A kẻ đường thẳng vuông góc với AM cắt Bx và Cy lần lượt tại P và Q. CM:
a) AP = BP và AQ = CQ
b) BC đi qua trung điểm I của AH
c) Khi BC cố định; BC = 2a, điểm a chuyển động sao cho góc BAC = 90°. Tìm vị trí của H trên đoạn thẳng BC để diện tích của ∆ABH max. Tìm giá trị max đó