cho tam giác ABC lấy điểm D đối xứng với B qua A, điểm E đối xứng với C qua B. Gọi I là giao điểm của AC và DE. Biết DE= a. Tính DI theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2022
a: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)
c: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường trung trực
nên AB là tia phân giác của góc DAE(1)
Ta có: D và F đối xứng nhau qua AC
nên AC là đường trung trực của DF
=>AD=AF
=>ΔADF cân tại A
mà AC là đường trung trực của DF
nên AC là tia phân giác của góc DAF(2)
Từ (1) và (2) suy ra \(\widehat{FAE}=2\cdot\left(\widehat{BAD}+\widehat{CAD}\right)=2\cdot90^0=180^0\)
Do đó: F,A,E thẳng hàng
13 tháng 4 2023
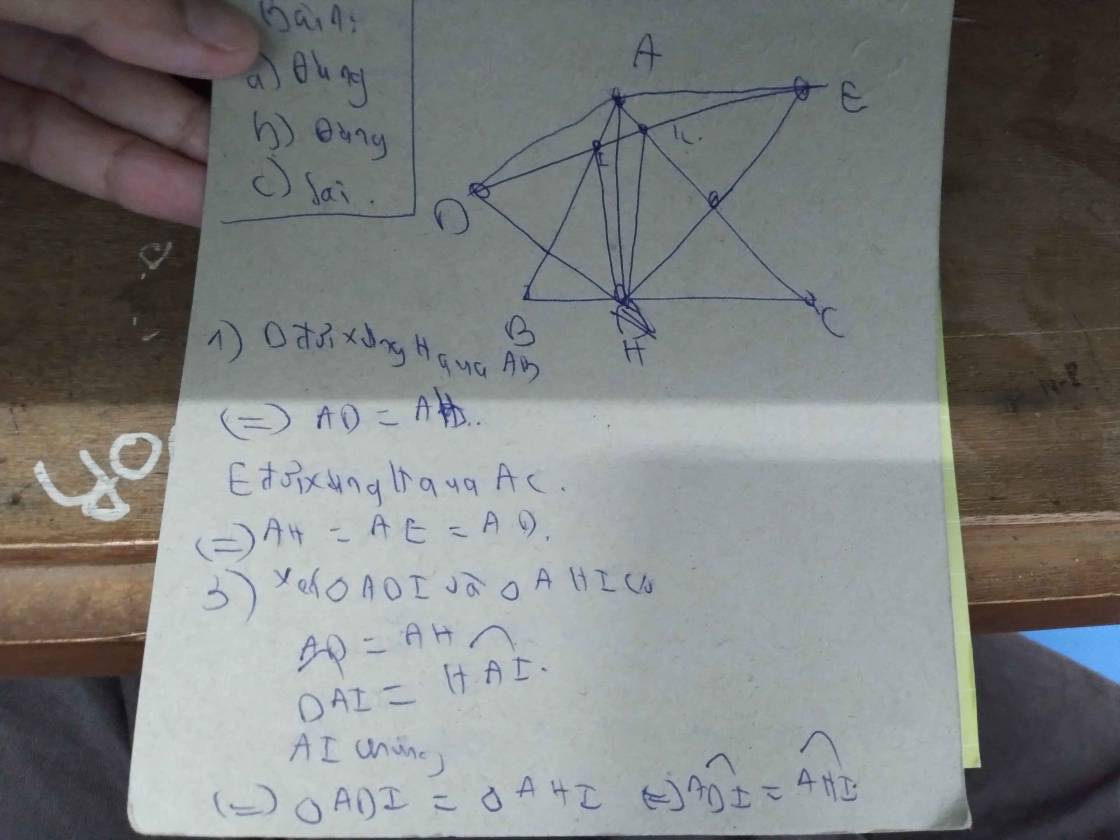
1: H đối xứng D qua AB
=>AH=AD
H đối xứng E qua AC
=>AH=AE
=>AH=AD=AE
3: Xét ΔAIH và ΔADI có
AH=AD
góc HAI=góc DAI
AIchung
=>ΔAIH=ΔAID
=>góc AHI=góc ADI=góc ADE
Xét ΔAHK và ΔAEK có
AH=AE
góc HAK=góc EAK
AK chung
=>ΔAHK=ΔAEK
=>góc AEK=góc AHK=góc AED
=>góc AHK=góc AHI
=>HA là phân giác của góc IHK
TN
21 tháng 8 2015
a) -cm AB va AC la trung truc DH va HE
-cm tam giac AMD= tam giac AMH ( c-g-c-) : AD=AH ( A thuoc trung truc DH) .AM=AM canh chung , DM=MH ( M thuoc trung truc DH)
cmtt tam giac AHN=tam giac ANE
--> AM va AN la p.g goc DAH va goc HAE
==> goc DAH+ HAE= goc DAE--> 2 goc MAH+ 2 goc HAN= goc DAE
--> 2 ( goc MAH+goc HAN )= goc DAE--> goc DAE=2. goc A=2.60=120
ta co : goc DAE+ goc ADE+ goc AED=180 ( tong 3 goc trong tam giac )
--> gocADE+ AED=180- goc DAE=180-120=60
ma ADE = goc MHA va goc AED= goc AHN ( 2 cap tam giac bang nhau cmt)
nen goc MHA+goc AHN=60--> goc MHN=60
