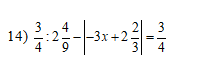 mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng
mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

Tam giác ABC vuông tại A
=>AB=AC ( 2 cạnh góc vuông của tam giác vuông cân)
BC là cạnh huyền
=> BC^2=AB^2+BC^2=2AB^2 (do AB=BC)
=2a^2
=> BC= \(\sqrt{2}a\)










\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{9}{22}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\\ \Rightarrow\left|-3x+\dfrac{8}{3}\right|=\dfrac{11}{6}-\dfrac{3}{4}=\dfrac{13}{12}\\ \Rightarrow\left[{}\begin{matrix}-3x+\dfrac{8}{3}=\dfrac{13}{12}\\3x-\dfrac{8}{3}=\dfrac{13}{12}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}3x=\dfrac{19}{12}\\3x=\dfrac{15}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{19}{36}\\x=\dfrac{5}{4}\end{matrix}\right.\)
\(\dfrac{3}{4}:2\dfrac{4}{9}-\left|-3x+2\dfrac{2}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{3}{4}:\dfrac{22}{9}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{27}{88}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\left|-3x+\dfrac{8}{3}\right|=-\dfrac{39}{88}\left(VLý\right)\)
Vậy \(S=\varnothing\)