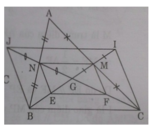
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại I
a) Chứng minh : MN // BC
b) Trên tia đối của tia MI llaays điểm K sao cho MK = MI. Tứ giác AKCI là hình gì? Vì sao?
c) Gọi P là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua điểm I. Chứng minh : I, P, D thẳng hàng.
d) Tìm điều kiện của tam giác ABC để tứ giác AKCI có đường chéo AC là phân giác của góc IAK.

 ien/nhu140826 và https://olm.vn/thanhvien/trungkienhy79
ien/nhu140826 và https://olm.vn/thanhvien/trungkienhy79


a) ∆ABC có M, N lần lượt là trung điểm của AC, AB (gt) nên MN là đường trung bình của tam giác => MN // BC
b) Tứ giác AKCI có hai đường chéo IK và AC cắt nhau tại trung điểm của mỗi đường (AM = MC, IM = MK) nên là hình bình hành
c) ∆ABC có BM và CN là hai đường trung tuyến và P là trung điểm của BC nên AP là đường trung tuyến thứ ba => A, I, P thẳng hàng
Mà A, I, D thẳng hàng nên I, P, D thẳng hàng (đpcm)
d) Tứ giác AKCI là hình bình hành có đường chéo AC là phân giác của góc IAK nên là hình thoi => AC vuông góc IK
Do đó tam giác ABC phải cân tại B (có BM là đường cao cũng là trung tuyến)
Ở câu a từ trung tuyến suy ra được trung điểm luôn ah bạn?