Giải phương trình: ( 1 + cos2x )cosx + ( 1 + cos2x )sinx = 1 + sin2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2022
\(cos2x+cosx+1=sin2x+sinx\)
\(\Leftrightarrow cos^2x-sin^2x+cosx+cos^2x+sin^2x=2sinx.cosx+sinx\)
\(\Leftrightarrow2cos^2x+cosx=2sinx.cosx+sinx\)
\(\Leftrightarrow cosx\left(2cosx+1\right)=sinx\left(2cosx+1\right)\)
\(\Leftrightarrow\left(2cosx+1\right)\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sinx=cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\tanx=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{4}+k\pi\\\end{matrix}\right.\)
PT
1
2 tháng 8 2021
Pt <=> 2sin\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\) = 2cos\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\)
⇔ cos\(\dfrac{x}{2}\) . \(\left(sin\dfrac{3x}{2}-cos\dfrac{3x}{2}\right)\) = 0
⇔ \(\sqrt{2}sin\left(\dfrac{3x}{2}-\dfrac{\pi}{4}\right).cos\dfrac{x}{2}=0\)
⇔
PT
1
CM
26 tháng 2 2018
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
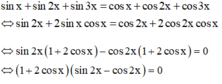
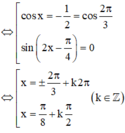
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
HP
24 tháng 12 2021
\(\sqrt{3}cos2x-sin2x=\sqrt{3}sinx+cosx\)
\(\Leftrightarrow\sqrt{3}cos2x-\sqrt{3}sinx-sin2x-cosx=0\)
\(\Leftrightarrow\sqrt{3}\left(1-2sin^2x-sinx\right)-2sinx.cosx-cosx=0\)
\(\Leftrightarrow-\sqrt{3}\left(sinx+1\right)\left(2sinx-1\right)-cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left[\sqrt{3}\left(sinx+1\right)+cosx\right]=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(\sqrt{3}sinx+cosx+\sqrt{3}\right)=0\)
\(\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
HP
1 tháng 6 2021
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
HP
1 tháng 6 2021
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
MA
0
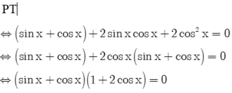
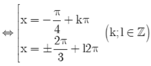
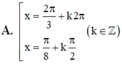
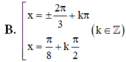
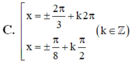
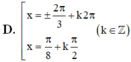
\(\Leftrightarrow\left(1+cos^2x\right)\left(sinx+cosx\right)=sin^2x+cos^2x+2sinx.cosx\)
\(\Leftrightarrow\left(1+cos^2x\right)\left(sinx+cosx\right)=\left(sinx+cosx\right)^2\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+cos^2x-sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\Rightarrow x=-\frac{\pi}{4}+k\pi\\1+cos^2x-sinx-cosx=0\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(\left\{{}\begin{matrix}sinx=a\\cosx=b\end{matrix}\right.\) với \(\left|a\right|;\left|b\right|\le1\) ta được hệ:
\(\left\{{}\begin{matrix}a^2+b^2=1\\1+b^2-a-b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2=1\\a=b^2-b+1\end{matrix}\right.\)
\(\Rightarrow b^2+\left(b^2-b+1\right)^2=1\)
\(\Leftrightarrow b\left(b^3-2b^2+4b-2\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=0\Rightarrow a=1\Rightarrow x=\frac{\pi}{2}+k2\pi\\b^3-2b^2+4b+2=0\left(2\right)\end{matrix}\right.\)
Pt (2) là 1 pt ko giải được theo kiến thức phổ thông