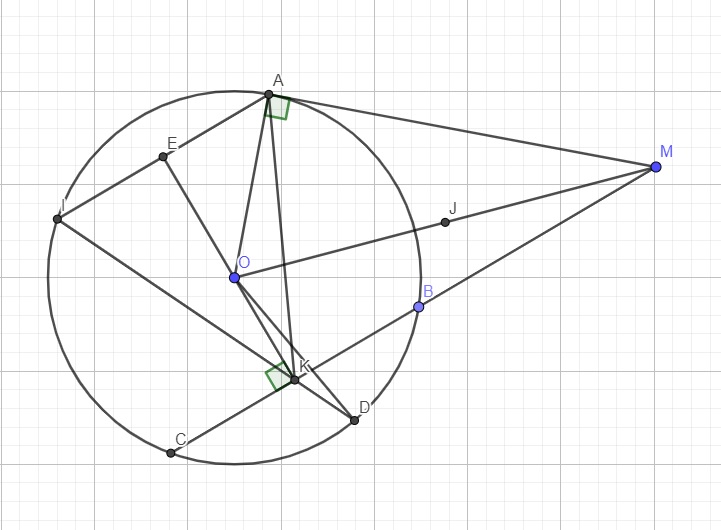
Cho góc xAy = 45 độ và điểm O nằm trong góc đó. Vẽ đường tròn (O; OA) cắt Ax và Ay thứ tự tại B và C. Vẽ đường tròn đường kính BC cắt Ax và Ay lần lượt ở M và N. Chứng minh rằng:
a) O là trực tâm của tam giác AMN;
b) \(MN=\frac{BC}{\sqrt{2}}\)
c) Tính tỉ số diện tích của hai tam giác ABC và AMN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Do MA là tiếp tuyến \(\Rightarrow AM\perp OA\Rightarrow\Delta OAM\) vuông tại A
\(\Rightarrow O,A,M\) cùng thuộc đường tròn đường kính OM
Do \(OK\perp BC\Rightarrow\Delta OKM\) vuông tại K
\(\Rightarrow O,K,M\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow M,A,O,K\) cùng thuộc đường tròn đường kính OM
Hay tứ giác MAOK nội tiếp đường tròn đường kính OM, với tâm là trung điểm J của OM và bán kính \(R=\dfrac{OM}{2}\)
b.
Do \(AI||BC\Rightarrow\widehat{IAK}=\widehat{AKM}\) (so le trong)
Lại có MAOK nội tiếp \(\Rightarrow\widehat{AKM}=\widehat{AOM}\) (cùng chắn cung AM)
\(\Rightarrow\widehat{IAK}=\widehat{AOM}\) (1)
Mà \(\widehat{AOM}+\widehat{AMO}=90^0\) (\(\Delta OAM\) vuông tại A theo c/m câu a)
\(\Rightarrow\widehat{IAK}+\widehat{AMO}=90^0\)
c.
Gọi E là trung điểm AI \(\Rightarrow OE\perp IA\)
Mà \(IA||BC\Rightarrow OE\perp BC\Rightarrow O,E,K\) thẳng hàng
\(\Rightarrow KE\) đồng thời là đường cao và trung tuyến trong tam giác KAI
\(\Rightarrow\Delta KAI\) cân tại K \(\Rightarrow\widehat{AIK}=\widehat{IAK}\) \(\Rightarrow\widehat{AIK}=\widehat{AOM}\) (theo (1))
Mặt khác \(\widehat{AIK}\) và \(\widehat{AOD}\) là góc nội tiếp và góc ở tâm cùng chắn cung AD của (O)
\(\Rightarrow\widehat{AIK}=\dfrac{1}{2}\widehat{AOD}\Rightarrow\widehat{AOM}=\dfrac{1}{2}\left(\widehat{AOM}+\widehat{MOD}\right)\)
\(\Rightarrow\widehat{AOM}=\widehat{MOD}\)
Xét hai tam giác AOM và DOM có:
\(\left\{{}\begin{matrix}OM\text{ chung}\\\widehat{AOM}=\widehat{MOD}\left(cmt\right)\\AO=DO=R\end{matrix}\right.\) \(\Rightarrow\Delta AOM=\Delta DOM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODM}=\widehat{OAM}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến của (O)

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được

Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).
a) M,N thuộc đường tròn đường kính BC=> Tam giác BMC và tam giác BNC vuông tại M,N
Mà \(\widehat{MAN}=45\Rightarrow\)Tam giác MAC và tam giác NAB vuông cân tại M,N
Khi đó: \(\hept{\begin{cases}OA=OC\\MA=MC\end{cases}\Rightarrow}\)OM là đường trung trực của AC \(\Rightarrow OM\perp AC\)
\(\hept{\begin{cases}OA=OB\\NA=NB\end{cases}\Rightarrow}\)ON là đường trung trực của AB \(\Rightarrow ON\perp AB\)
Vậy O là trực tâm tam giác ABC.
b) \(B,C\in\left(O,OA\right)\Rightarrow OB=OC\)
O thuộc đường tròn đường kính BC=> Tam giác OBC vuông cân tại O \(\Rightarrow\widehat{OBC}=45\)
Tam giác NBA vuông cân tại N \(\Rightarrow\widehat{NBA}=45\)
Vì \(\widehat{OBC}=\widehat{NBA}\) là các góc tại B chắn các cung nhỏ OC và MN của đường tròn đường kính BC \(\Rightarrow MN=OC=BCcos45=\frac{BC}{\sqrt{2}}\)
c) \(\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}AM.AN.sin\widehat{MAN}}{\frac{1}{2}AB.AC.sin\widehat{BAC}}=\left(\frac{AM}{AC}\right)\left(\frac{AN}{AB}\right)=cos\widehat{MAN}.cos\widehat{BAC}=cos^245=\frac{1}{2}\)