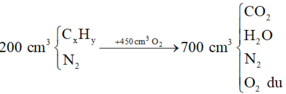
Cho 400ml một hỗn hợp gồm nito và hidrocacbon vào 900ml oxi dư rồi đốt.thể tích hỗn hợp thu được sau khi đốt là 1,4 lít. Sau khi cho nước ngưng tụ còn 800ml hỗn hợp, người ta cho lội qua dung dịch KOH thấy còn 400ml khí. Các thể tích đều đo ở cùng điều kiện nhiệt độ, áp suất. Công thức phân tử của HCHC là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2023
Ta có: \(V_{H_2O}=1400-800=600\left(ml\right)\)
\(V_{O_2\left(dư\right)}+V_{N_2}=400\left(ml\right)\)
\(\Rightarrow V_{CO_2}=800-400=400\left(ml\right)\)
BTNT O, có: \(V_{O_2\left(pư\right)}=\dfrac{2V_{CO_2}+V_{H_2O}}{2}=700\left(ml\right)\)
\(\Rightarrow V_{O_2\left(dư\right)}=900-700=200\left(ml\right)\) \(\Rightarrow V_{N_2}=400-200=200\left(ml\right)\)
\(\Rightarrow V_{C_xH_y}=400-200=200\left(ml\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{V_{CO_2}}{V_{C_xH_y}}=2\\y=\dfrac{2V_{H_2O}}{V_{C_xH_y}}=6\end{matrix}\right.\)
Vậy: CTPT của X là C2H6.
3 tháng 8 2017
Đáp án C
Quan sát 4 đáp án ta có công thức của X có dạng CxHy
19 tháng 3 2022
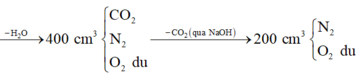
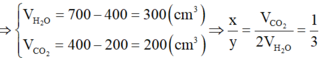
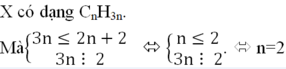
Y gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:b\left(mol\right)\\H_2O:c\left(mol\right)\end{matrix}\right.\)
Z gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:b\left(mol\right)\end{matrix}\right.\)
Do nZ = 50%.nY
=> a + b = 0,5a + 0,5b + 0,5c
=> \(c=a+b\)
Khí thoát ra khỏi dd NaOH là khí A
\(n_{CO_2}=83,33\%.n_Z\)
=> b = 0,8333.(a + b)
=> 5a = b
=> Y gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:5a\left(mol\right)\\H_2O:6a\left(mol\right)\end{matrix}\right.\)
=> nC(A pư) : nH(A pư) = 5a : 12a = 5 : 12
=> CTPT: (C5H12)n
Chọn n = 1 thỏa mãn => CTPT: C5H12
làm sao biết được đó là ankan và Nito có phản ứng với O2 ra NO mà ?
Giả sử các khí đều đo ở đktc
\(CTHH:C_nH_{2n+2}\)(n là số tự nhiên khác 0)
\(V_{H_2O}=1,4-0,8=0,6\left(l\right)\)
\(V_{CO_2}=0,8-0,4=0,4\left(mol\right)\)
=> \(\left\{{}\begin{matrix}n_{H_2O}=\frac{0,6}{22,4}=\frac{3}{112}\left(mol\right)\\n_{CO_2}=\frac{0,4}{22,4}=\frac{1}{56}\left(mol\right)\end{matrix}\right.\)
Bảo toàn H: \(n_{H\left(X\right)}=2.n_{H_2O}=\frac{3}{56}\left(mol\right)\)
Bảo toàn C: \(n_{C\left(X\right)}=n_{CO_2}=\frac{1}{56}\left(mol\right)\)
=> \(\frac{n_C}{n_H}=\frac{\frac{1}{56}}{\frac{3}{56}}=\frac{1}{3}\) => \(\frac{n}{2n+2}=\frac{1}{3}=>n=2\)
=> CTHH: \(C_2H_6\)