cho tam giác ABC vuông tại A , AB= 6cm, AC= 8cm. Các đường trung tuyến AN và CM cắt nhau tại G. Hãy tính AG và MG
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BC=căn 8^2+6^2=10cm
=>AD=5cm
AG=2/3*5=10/3cm
GD=5-10/3=5/3cm

a) Xét \(\Delta ABC\)có : \(AB=AC\Rightarrow\Delta ABC\)cân
Có BM và CN là đường trung tuyến của tam giác \(\Rightarrow AM=AN=BN=CN\)
Xét \(\Delta AMB\)và \(\Delta ANC\)có : \(\hept{\begin{cases}AM=AN\left(cmt\right)\\\widehat{mAn}:chung\\AB=AC\left(gt\right)\end{cases}\Rightarrow\Delta AMB=\Delta ANC\left(c\cdot g\cdot c\right)}\)
b) Vì 2 đường trung tuyến BM và CN cắt nhau tại G => G là trọng tâm của \(\DeltaÂBC\)
=> AG là đường trung tuyến còn lại
mà \(\Delta ABC\)cân => AG vừa là đường trung tuyến và vừa là đường cao
\(\Rightarrow AG\perp BC\)hay \(AH\perp BC\)

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100\)
hay BC=10cm
Xét ΔABC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=8
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
c: Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)
\(\widehat{BAI}=\widehat{BCD}\left(=90^0-\widehat{ABH}\right)\)
Do đó: ΔABI\(\sim\)ΔCBD
d: Xét ΔBHA có BI là đường phân giác ứng với cạnh AH
nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\left(1\right)\)
Xét ΔBAC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)
Ta có: \(AB^2=BH\cdot BC\)
nên \(\dfrac{BH}{BA}=\dfrac{AB}{BC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)

a. Áp dụng đinh lí Py - ta - go vào Δ ABC vuông tại A:
BC2 = AC2 + AB2
BC2 = 122 + 92 = 144 + 81 = 225
=> BC = 15 cm (BC > 0)
câu b mik chưa biết làm. Sorry bạn :(

Vì BM là đường phân giác của góc B nên ta có:
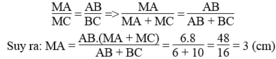
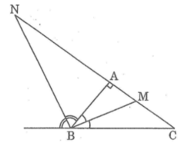
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: BM ⊥ BN
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: A B 2 = AM.AN
Suy ra: AN = ![]() = 12 (cm)
= 12 (cm)
Bài giải
Vì M là trung điểm của AB nên MA = MB = 6 : 2 = 3 cm
Trong tam giác AMG vuông tại A có :
\(MA^2+AC^2=MC^2\)
\(3^2+8^2=MC^2=73\)
\(\Rightarrow\text{ }MC=\sqrt{73}\text{ }cm\)
Ta có : \(MG=\frac{1}{3}MC=\frac{\sqrt{73}}{3}\)
còn AG nữa bạn