Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta dễ thấy rằng các cường độ điện trường thành phần do các điện tích gây ra tại O chỉ khác nhau về chiều và có cùng độ lớn:
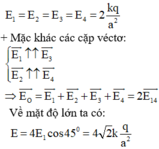

Đáp án A
+ Ta dễ thấy rằng các cường độ điện trường thành phần do các điện tích gây ra tại O chỉ khác nhau về chiều và có cùng độ lớn:
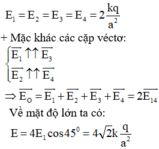

Đáp án: A
+ Ta dễ thấy rằng các cường độ điện trường thành phần do các điện tích gây ra tại O chỉ khác nhau về chiều và có cùng độ lớn:
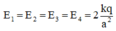
+ Mặc khác các cặp véctơ:
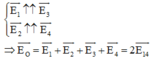
Về mặt độ lớn ta có:
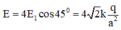

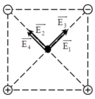
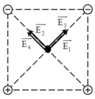
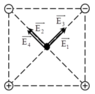
Các điện tích đặt tại các đỉnh của hình vuông gây ra tại giao điểm O của hai đường chéo hình vuông các véc tơ cường độ điện trường E A → , E B → , E C → , E D → ; có phương chiều như hình vẽ.
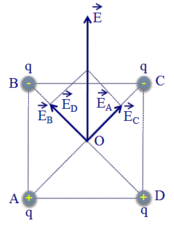
Có độ lớn: EA = EB = EC = ED = 2 k q ε a 2 .
Cường độ điện tường tổng hợp tại O là: E → = E A → + E B → + E C → + E D → ; có phương chiều như hình vẽ; có độ lớn: E = 4 E A cos 45 ° = 4 2 k q ε a 2
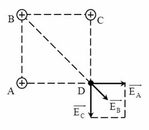

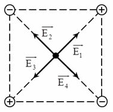

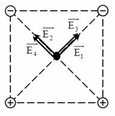

- Gọi F1, F2, F3, F4 lần lượt là lực do Q đặt tại 4 đỉnh A, B, C, D của hình vuông tác dụng lên điện tích q đặt tại tâm của hình vuông.
-Hợp lực tác dụng lên q là:\(\overrightarrow{F}=\overrightarrow{F1}+\overrightarrow{F2}+\overrightarrow{F3}+\overrightarrow{F4}=\left(\overrightarrow{F1}+\overrightarrow{F3}\right)+\left(\overrightarrow{F2}+\overrightarrow{F4}\right)\left(1\right)\)
Để q nằm cân bằng thì: \(\overrightarrow{F}=\overrightarrow{0}\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{F1}+\overrightarrow{F3}=0\\\overrightarrow{F2}+\overrightarrow{F4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{F1}=-\overrightarrow{F3}\\\overrightarrow{F2}=-\overrightarrow{F4}\end{matrix}\right.\)(2)
➞ q có thể dương hoặc âm.
- Xét cân bằng của điện tích Q tại đỉnh B (hoặc A, C, D):
\(\overrightarrow{F12}+\overrightarrow{F32}+\overrightarrow{F42}+\overrightarrow{F02}=0\Rightarrow\overrightarrow{F12}+\overrightarrow{F32}+\overrightarrow{F42}=-\overrightarrow{F02}\)
➞ q < 0
➞ \(k\frac{Q^2}{a^2}.\sqrt{2}+k\frac{Q^2}{2a^2}=k\frac{\left|qQ\right|}{\frac{a^2}{2}}\Rightarrow q=-\frac{Q}{4}\left(2\sqrt{2}+1\right)\)