a) a2 + 9 - 6a
b) x2 - x + 1/4
c) -x2 + 4x - x
Vận dụng hằng đẳng thức, thu gọn các biểu thức sau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 6 2019
Hoàn thiện HĐT ta thu được các đơn thức cần điền vào “…”.
a) x 2 + 4x + 4 = ( x + 2 ) 2 . b) 4 x 2 – 12x + 9 = ( 2 x – 3 ) 2 .
c) 4 x 2 – 12xy + 9 y 2 = ( 2 x – 3 y ) 2 .
Chú ý: phép trừ ta chuyển thành cộng đại số.
d) x − y 2 x + y 2 = x 2 − y 2 4 .
16 tháng 9 2021
\(a,=\left(x+1\right)^2\\ b,=\left(y-2\right)^2\\ c,=\left(x-3\right)^2\\ d,=\left(a-7\right)^2\\ e,=\left(m-2\right)^2\\ f,=\left(2x-1\right)^2\\ g,=\left(a+5\right)^2\\ h,=\left(z-10^2\right)\\ i,=\left(x+3y\right)^2\\ j,=\left(2x-5b\right)^2\\ k,=\left(a+5\right)^2\\ l,=\left(x^2+1\right)^2\\ m,=\left(y^3-1\right)^2=\left(y-1\right)^2\left(y^2+y+1\right)^2\\ n,=\left(c^5-5\right)^2\\ o,=\left(3x^2+2y\right)^2\\ p,=5m^2n^3\left(5m^2n^3-2\right)\)
CM
20 tháng 8 2019
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm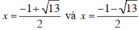 
Ta có bảng xét dấu sau:
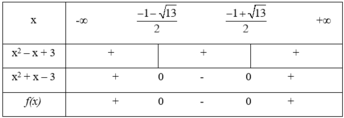
Kết luận:
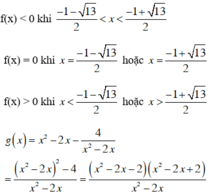
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
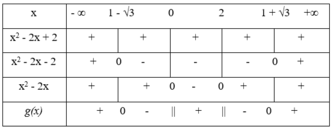
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
15 tháng 9 2021
a) \(=\left(x-2\right)^2\)
b) \(=\left(3x-2\right)^2\)
c) \(=\left(x-3y\right)^2\)
d) \(=\left(\dfrac{x}{2}+1\right)^2\)
e) \(=\left(x-4\right)^2\)
f) \(=\left(\dfrac{1}{2}xy^2+1\right)^2\)
g) \(=\left(x-1\right)\left(x+1\right)\)
h) \(=\left(5x-4\right)\left(5x+4\right)\)
KV
27 tháng 12 2022
a) ĐKXĐ: 3x + 6 khác 0
x khác -2
b) A = (x² + 4x + 4)/(3x + 6)
= (x + 2)²/[3(x + 2)]
= (x + 2)/3
c) Khi x = 1/4, ta có:
A = (1/4 + 2)/3
= (9/4)/3
= 3/4
Bài giải
\(a,\text{ }a^2+9-6a=a^2+2\cdot3a+3^2=\left(a-3\right)^2\)
\(b,\text{ }x^2-x+\frac{1}{4}=x^2-2\cdot\frac{1}{2}\cdot x+\left(\frac{1}{2}\right)^2=\left(x-\frac{1}{2}\right)^2\)
\(c,\text{ }-x^2+4x-x=3x-x^2=\left(\sqrt{3x}\right)^2-x^2=\left(\sqrt{3x}-x\right)\left(\sqrt{3x}+x\right)\)( Đề nói vận dụng hằng đẳng thức để rút gọn nên mình đưa về hiệu hai ình phương nha ! )
a) \(a^2+9-6a\)
\(=\left(a-3\right)^2\)
b) \(x^2-x+\frac{1}{4}\)
\(=\left(x-\frac{1}{2}\right)^2\)
c) \(-x^2+4x-x\)
\(=3x-x^2\)
\(=x\left(3-x\right)\)