Cho tam giác ABC vuông tại A, đường cao AH = \(2\sqrt{3}\) cm và chân đường cao H chia cạnh huyền thành hai đoạn c’ và b’ mà \(\frac{c'}{b'}=\frac{1}{3}\) . Tính độ dài ba cạnh của tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)

Xét hai tam giác vuông ABH và CAH có:
∠ ABH = ∠ CAH (cùng phụ với góc ∠ BAH)
Do đó △ ABH đồng dạng △ CAH (g.g).
Suy ra: 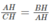
⇒ A H 2 = BH. CH = 4.9 = 36 ⇒ AH = 6(cm)
Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.
Suy ra: DE = AH = 6 (cm)

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

Theo chứng minh trên, ta có:
DM = MH = 1/2 BH = 1/2.4 = 2(cm)
EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)
DE = AH = 6(cm)
DENM là hình thang vuông, do đó diện tích của nó là:
S D E N M = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5( c m 2 ).

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)

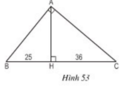
+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
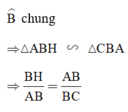
⇒AB2=BH.BC=25.(25+36)=1525


a.Tu gia thuyet suy ra:\(AC=20\left(cm\right)\)
Ta co:\(AH=\frac{AB.AC}{\sqrt{AB^2+AC^2}}=\frac{15.20}{\sqrt{15^2+20^2}}=20\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{225+400}=\sqrt{625}=25\left(cm\right)\)
b.Ta co:\(BH=\frac{AB^2}{BC}=\frac{225}{25}=9\left(cm\right)\)
\(CH=\frac{AC^2}{BC}=\frac{400}{25}=16\left(cm\right)\)
a)Ta có: AB/AC=3/4 =)AC=4*AB/3=4*15/3=2
áp dụng đjnh lí Pytago tong tam giác vuông ABC, ta có:
BC^2=AB^2+AC^2
=15^2+20^2
= 225+400
=625
BC = căn 625=25
Vì ABC là tam giác vuông nên
áp dụng hệ thức lượng, ta dc
AB^2=HB*BC
hay 15^2=HB*25
HB=225/25=9
=)HC=25-9=16
và AH^2=HB*HC
=9*16=144
AH=căn 144=12
câu b là đoạn từ vì tam ABC đến HC=16 NHÉ BN
MK vẽ hình hơi xấu bn thông cảm hihi

Ta có : HB + HC = BC = 8 cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=2.8\Rightarrow AB=4cm\)
* Áp dụng hệ thức : \(AC^2=CH.BC=6.8\Rightarrow AC=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{16\sqrt{3}}{8}=2\sqrt{3}cm\)
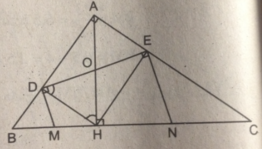
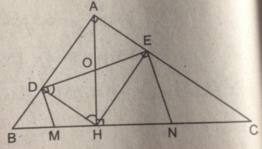
Xét \(\Delta\)ABC có :
AH2 = BH.CH
AH2 = c'.b' (1)
Mà c'/b' = 1/3
=》3c' = b
Thay vào (1) ta có :
12 = c'.3c'
12 = 3c'2
c'2 = 4
=》 c' = 2 (cm)
=》b' = 3.2 = 6(cm)
=》 BC = 2 + 6 = 8 (cm)
Ta có : AB2 = BH.BC = 2.8 = 16
=》 AB = 4(cm)
Lại có AC2 = CH.BC = 6.8 = 48(cm)
=》 AC = 4\(\sqrt{ }\)3 (cm)