cho tam giác ABC có M là trung điểm của BC,AM là tia phân giác của góc BAC
a)chứng minh tam giác ABC cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 1 2022
Tham khảo:
Xét tam giác `ABM` và tam giác `AMC`, ta có :
AM cạnh huyền chung
\(\widehat{AMB}=\widehat{AMC}=90^o\)(góc vuông )
\(\widehat{BAM}=\widehat{MAC}\)(giả thiết)
Do đó tam giác `ABM`=tam giác `AMC`(cạnh huyền-cạnh góc vuông)
\(=>AB=AC\)(hai cạnh tương ứng)
=>tam giác `ABC` cân tại `A.`
17 tháng 12 2021
\(a,\left\{{}\begin{matrix}AB=AC\\\widehat{BAM}=\widehat{CAM}\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta BAM=\Delta CAM\left(c.g.c\right)\\ b,\Delta BAM=\Delta CAM\\ \Rightarrow MB=MC\\ \Rightarrow M\text{ là trung điểm }BC\\ c,\Delta BAM=\Delta CAM\\ \Rightarrow\widehat{AMB}=\widehat{AMC}\\ \text{Mà }\widehat{AMB}+\widehat{AMC}=180^0\\ \Rightarrow\widehat{AMB}=90^0\\ \Rightarrow AM\bot BC\)
CM
1 tháng 8 2018
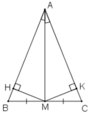
Kẻ MH ⊥ AB, MK ⊥ AC
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) = 90o
Cạnh huyền AM chung
∠(HAM) = ∠KAM) (gt)
⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90o
MB = MC ( vì M là trung điểm BC).
MH = MK (chứng minh trên)
⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.
Xét \(\Delta ABC\)có
AM là đường trung tuyến ( M là trung điểm của BC )
AM là đường phân giác ( AM là tia phân giác của \(\widehat{BAC}\))
Nên \(\Delta ABC\)cân tại A ( tam giác có đường trung tuyến đồng thời là đường phân giác )
Vì M là trung điểm của BC
=> AM là đường trung tuyến của BC
ta có AM là đường trung tuyến vừa là tia phân giác
=> Tam giác ABC cân tại A