Cho đa thức P(x)= x^4+mx^3-55x^2+nx-156 chia hết cho x-2 và chia hết cho x-3. Hãy tìm giá trị của m,n rồi tìm tất cả các nghiệm của đa thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có f(x) - 5 \(⋮\)x + 1
=> x3 + mx2 + nx + 2 - 5 \(⋮\)x + 1
=> x3 + mx2 + nx - 3 \(⋮\)x + 1
=> x = - 1 là nghiệm đa thức
Khi đó (-1)3 + m(-1)2 + n(-1) - 3 = 0
<=> m - n = 4 (1)
Tương tự ta được f(x) - 8 \(⋮\)x + 2
=> x3 + mx2 + nx - 6 \(⋮\) x + 2
=> x = -2 là nghiệm đa thức
=> (-2)3 + m(-2)2 + n(-2) - 6 = 0
<=> 2m - n = 7 (2)
Từ (1)(2) => HPT \(\left\{{}\begin{matrix}m-n=4\\2m-n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n=-1\end{matrix}\right.\)
Vậy đa thức đó là f(x) = x3 + 3x2 - x + 2
b) f(x) - 7 \(⋮\)x + 1
=> x3 + mx + n - 7 \(⋮\) x + 1
=> x = -1 là nghiệm đa thức
=> (-1)3 + m(-1) + n - 7 = 0
<=> -m + n = 8 (1)
Tương tự ta được : x3 + mx + n + 5 \(⋮\)x - 3
=> x = 3 là nghiệm đa thức
=> 33 + 3m + n + 5 = 0
<=> 3m + n = -32 (2)
Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}3m+n=-32\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m=-40\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-10\\n=-2\end{matrix}\right.\)
Vậy f(x) = x3 - 10x -2

A(x) chia hết cho (x-2) và (x-3) => A(2)=0 và A(3)=0
\(\left\{{}\begin{matrix}2^4+8m-220+2n-156=0\\3^4+27m-495+3n-156=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8m+2n=360\\27m+3n=570\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\172\end{matrix}\right.\)
b) \(A\left(x\right)=x^4+2x^3-55x^2+172x-156\)
\(A\left(x\right)=\left(x-2\right)\left(x-3\right)\left(x^2+7x+6\right)\)
Giải \(x^2+7x-26\) được \(x_1=\dfrac{-7+3\sqrt{17}}{2};x_2=\dfrac{-7-3\sqrt{17}}{2}\)
Vậy \(S=\left\{2;3;\dfrac{-7\pm3\sqrt{17}}{2}\right\}\)

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
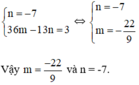

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
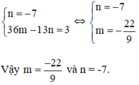

http://lazi.vn/edu/exercise/biet-rang-da-thuc-px-chia-het-cho-da-thuc-x-a-khi-va-chi-khi-pa-0-hay-tim-cac-gia-tri-cua-m-va-n

P(x) chia hết cho x - 2
=> P(2) = 0
=> \(2^4+m.2^3-55.2^2+2n-156=0\)<=> 8m + 2n = 360 => 4m + n = 180
P(x) chia hết cho x - 3
=> P(3) = 0
=> \(3^4+m.3^3-55.3^2+3n-156=0\)<=> 27m + 3n = 570 => 9m + n = 190
=> ( 9m + n ) - ( 4m+ n ) = 190 - 180
=> 5m = 10
=> m = 2
=> 4.2 + n = 180 => n = 172
Vậy P(x) = \(x^4+2x^3-55x^2+172x-156\)
P(x) chia hết cho x-2<=>P(2)=24 + 8m - 220 +2n - 156 =0 (1)
P(x) chia hết cho x-3<= >P(3)=34 + 27m - 495 + 3n -156=0 (2)
Từ (1) và (2) suy ra:
{16+8m-220+2n-156=0 <=>8m+2n=360
{81+27m-495+3n-156=0 <=>27m+3n=570
Giair hệ phương trình ta được
m=2 và n=172
thay m,n vào P(x), ta được:
P(x)=x4+2x3-55x2+172x-156
<=>P(x)=(x-2)(x-3)(x2+7x+6)<=>P(x)=0
<=>[x-2=0 <=>x=2
[x-3=0 <=>x=3
[x2+7x+6=0 <=>x=-7+3√17 / 2 hoặc x=7-3√17 / 2