1. Cho tam giác ABC có góc A=90 độ. Đường cao AH. Trên cạnh BC lấy D sao cho BD=BA. Đường vuông góc với BC tại D cắt AC tại E a) So sánh AE và DE
b) CMR : Tia AD là tia phân giác của góc HAC
c) Đường phân giác góc ngoài đỉnh C cắt đường thẳng BC ở K. Tính BAK
d) CMR : AB + AC < BC + AH
e) So sánh HD và DC

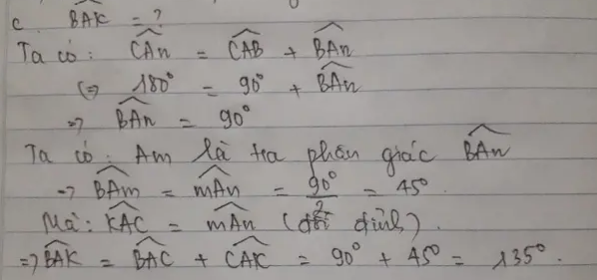
a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
a) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)