tô màu các đỉnh của một hình vuông ABCD bởi ba màu : xanh , đỏ , và vàng . Hỏi có bao nhiêu cách tô sao cho hai đỉnh kề nhau thì được tô màu khác nhau ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 12 2017
Đáp án A
TH1: 4 cạnh với 4 màu khác nhau, có A 6 4 = 360 cách.
TH2: 4 cạnh với 3 màu khác nhau, vì 2 cạnh giống màu không được kề nhau nên có 2 cách đặt vị trí cho 2 giống màu (đặt ở vị trí đối diện nhau). Tiếp theo, có 2! cách cho 2 màu còn lại. Vậy có C 6 3 . 3 .2.2 ! = 240
TH3: 4 cạnh với 2 màu khác nhau (giả sử xanh và đỏ), có 2 cách tô (AB=CD=xanh và AD=BC=đỏ/ hoặc AB=CD=đỏ và AD=BC=xanh) Trong trường hợp này có C 6 2 . 2 = 30 cách.
Vậy có tất cả 360 + 240 + 30 = 630 cách.
CM
10 tháng 8 2019
Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4 ! = 24 cách tô màu khác nhau
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô
Tổng cộng: 24. C 6 4 + 4.3 C 6 3 + 2. C 6 2 = 630 cách
CM
18 tháng 4 2019
Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4! = 24 cách tô màu khác nhau.
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô.
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô.
Tổng cộng: 24 . C 6 4 + 4 . 3 C 6 3 + 2 . C 6 2 = 630 cách.
CM
13 tháng 8 2018
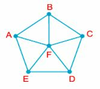
Tất cả các đỉnh A, B, C, D, E đều nối với đỉnh F nên đỉnh F phải tô màu khác với các đỉnh còn lại. Với 5 đỉnh còn lại thì A và C tô cùng một màu. B và D tô cùng một màu, E tô riêng một màu, như vậy cần ít nhất 3 màu để tô 5 đỉnh sao cho 2 đỉnh được nối bởi một cạnh được tô bởi 2 màu khác nhau. Vậy cần ít nhất 4 màu để tô 6 đỉnh của hình theo yêu cầu của đề bài.
CM
12 tháng 1 2017
Phương pháp giải:
Trong mỗi hình vuông nhỏ, tìm các hình tam giác và tứ giác rồi tô màu theo yêu cầu đề bài.
Chú ý : Ba hình đặt kề nhau thì có ba màu khác nhau.
Lời giải chi tiết:
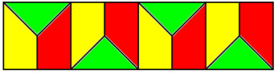
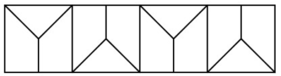
bạn ko có hình nè