cho f(x) = (2+x)1000 = ao + a1x + a2x2 + ....+ a1000x1000. Tìm hệ số lớn nhất trong khai triển
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715

Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
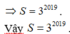

Đáp án A
Cho x = 1 vào 2 vế 3 x − 1 n = a 0 + a 1 x + a 2 x 2 + ... a n x n ta được 2 n = a 1 + a 2 + a 3 + ... + a n
Vậy n = 11 ⇒ a 6 = C 11 5 3 6 − 1 5 = − 336798
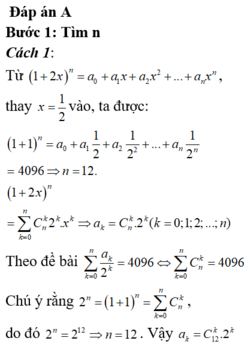
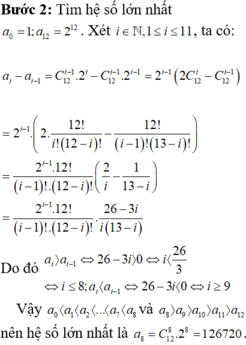
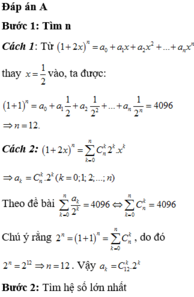
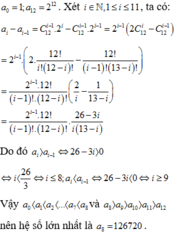
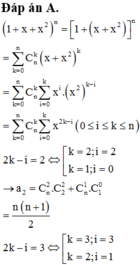
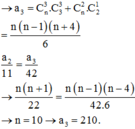
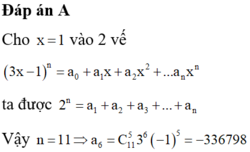

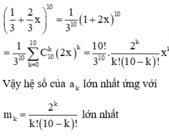


Số hạng tổng quát trong khai triển: \(C_n^k2^kx^{n-k}\) với \(n=1000\)
Hệ số của số hạng thứ k là: \(C_n^k2^k\)
Hệ số này là lớn nhất khi và chỉ khi: \(\left\{{}\begin{matrix}C_n^k2^k\ge C_n^{k+1}2^{k+1}\\C_n^k2^k\ge C_n^{k-1}2^{k-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{n!}{k!\left(n-k\right)!}\ge\frac{n!.2}{\left(k+1\right)!\left(n-k-1\right)!}\\\frac{n!.2}{k!\left(n-k\right)!}\ge\frac{n!}{\left(k-1\right)!\left(n-k+1\right)!}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k+1\ge2\left(n-k\right)\\2\left(n-k+1\right)\ge k\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}k\ge\frac{2n-1}{3}=\frac{1999}{3}\\k\le\frac{2n+2}{3}=\frac{2002}{3}\end{matrix}\right.\)
\(\Rightarrow k=667\)
Vậy hệ số lớn nhất là \(C_{100}^{667}2^{667}\)