Given a right prism ABC.A'B'C' that AB = 9 cm; BC = 15 cm; AC = 12 cm.
There are .... lines are perpendicular to the line AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
\(\widehat{A'BA}=60^0\Rightarrow AA'=AB.tan60^0=a\sqrt{3}\)
(Lại 1 bài mà sử dụng tọa độ hóa sẽ cho kết quả cực kì nhanh chóng).
Lớp 11 thì chắc phải dựng hình:
Trong mp (A'B'C'), qua C' kẻ đường thẳng song song A'B', qua B' kẻ đường thẳng song song A'C', hai đường thẳng này cắt nhau tại D'
\(\Rightarrow AC'||BD'\) (do tứ giác ABD'C' là hình bình hành)
\(\Rightarrow d\left(AC';A'B\right)=d\left(AC';\left(A'BD'\right)\right)=d\left(C';\left(A'BD'\right)\right)\)
Gọi giao điểm của A'D' và B'D' là O \(\Rightarrow OB'=OC'\) theo t/c 2 đường chéo hbh
\(\Rightarrow d\left(C';\left(A'BD'\right)\right)=d\left(B';\left(A'BD'\right)\right)\)
Quy được về 1 bài tính khoảng cách cơ bản: tứ diện B.A'B'D' có \(BB'\perp\left(A'B'D'\right)\) , tìm k/c từ B' đến mp (A'BD')
Lần lượt kẻ B'H vuông góc A'D' và B'K vuông góc BH thì B'K là k/c cần tìm
Bạn tự tính toán nốt nhé
11 tháng 12 2017
Đáp án B
Giải thích: Có hai cấu trúc khác nhau với từ “so” để chỉ mục đích
So as to + V(nguyên thể) = để làm gì đó
So that + mệnh đề = để mà
Sau phương án B là một mệnh đề, do đó ta cần dùng cáu trúc thứ hai.
Sửa lỗi: so as => so that
Dịch nghĩa: Một lăng kính được sử dụng để làm khúc xạ ánh sáng để nó tỏa ra trong một quang phổ nhiều màu sắc liên tục.
A. to retract (v) = khúc xạ
C. spreads out = tỏa ra, lan ra
D. of colors = của nhiều màu sắc
CM
28 tháng 4 2017
Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:
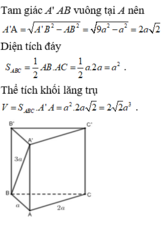
Lời giải:
Từ số liệu đề ta thấy $AB^2+AC^2=BC^2$ nên $AB\perp AC$ theo định lý Pitago đảo.
$\Rightarrow AB$ cũng vuông góc với $A'C'$
$ABC.A'B'C'$ là lăng trụ đứng nên $AB\perp BB', AA', CC'$
Vậy $AB$ vuông góc với 5 đường thẳng.