Question

[Hiền Lê]

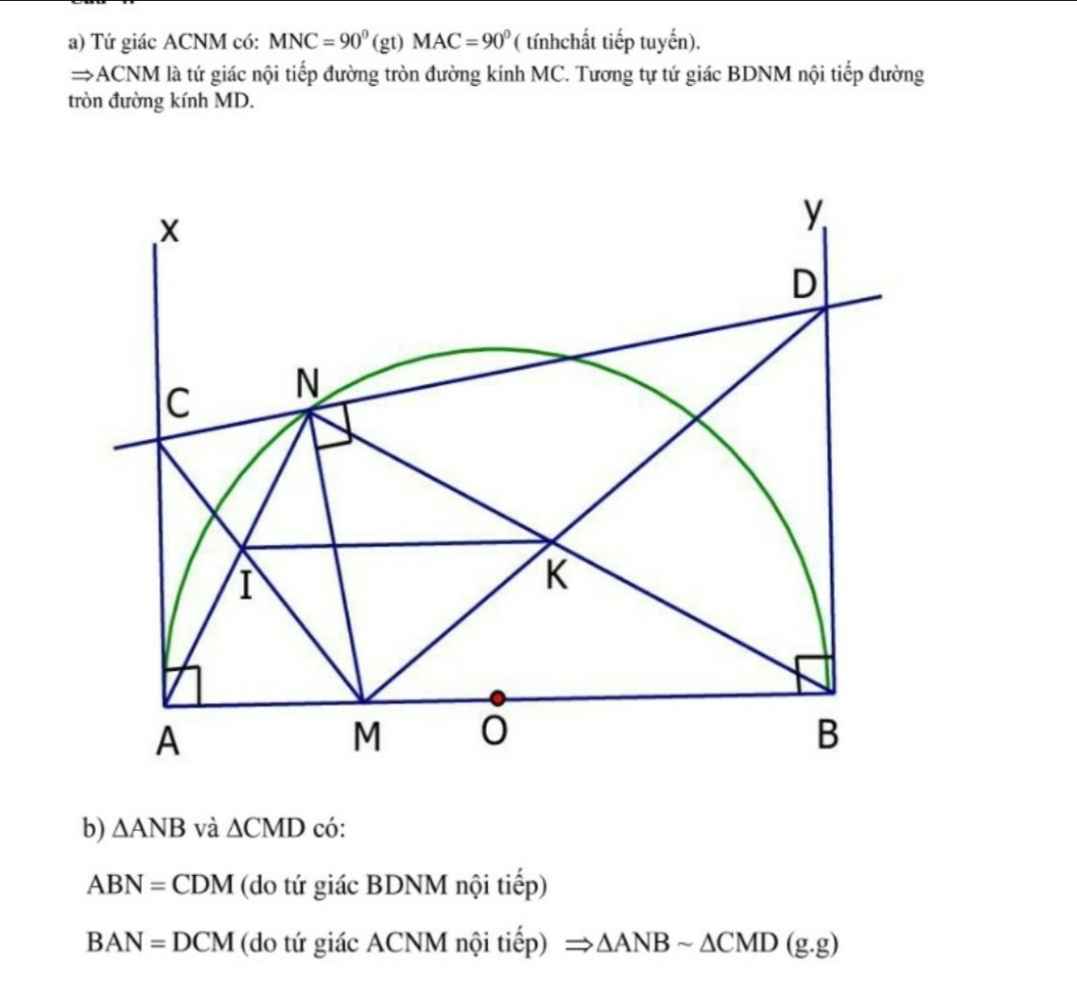
cho nửa đường tròn tâm (O) đường kính AB. lấy diểm M thuộc đoạn thẳng OA, điểmN thuộc nửa đường tròn (O). từ A và B vẽ các tiếp tuyến Ax,By. đường thẳng qua N và vuông góc với MN cắc Ax, By thứ tự tại C và D.

a) chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn

b) chứng minh tam giác ANB đồng dạng với tam giác CMB

C) gọi I là giao điểm của AN và CM , K là giao điểm của BN và DM . chưng minh IK song song AB

Answer 1

[Ĵ❍ƙĔŔᵛᶰ(*•.¸♡ţęąɱ ƒŗęę ƒįŗę❤☆)]

a, xét từ giác AMNC có 
$={90}^{\circ }$ (Ac là tiếp tuyến của (O) , $\stackrel{}{}$

${}^{}={90}^{\circ }$ (MN vuông góc với CD) => $\stackrel{}{}$\(\widehat{CAM}+\widehat{CNM}\)=180

=> AMNC nội tiếp

Xét tứ giác BMND có $\stackrel{ˆ}{}$=90 ( BD là tiếp tuyến của (O) , \(\widehat{CND}\)=90 ( MN vuông góc với CD)

=> \(\widehat{MND}+\widehat{NAC}\)=180

=> Tứ giác BDMN nội tiếp

b, Ta có \(\widehat{CMN}=\widehat{NAC}\) (cùng chắn CN)

=> ${\mathrm{\backslash (\backslash widehat\{CMN\}\backslash )}}^{}$=$\frac{1}{2}$ cung AN(1)

Ta cũng có\(\widehat{NMD}+\widehat{NMD}\) (cùng chắn cung ND)

\(\widehat{NMD}\)=$\frac{1}{2}$ cung NB(2)

Từ (1) và (2) => \(\widehat{CMD}+\widehat{NMD}\)= $\frac{1}{2}$ (cung AN + cung NB) 

=> \(\widehat{CMD}\)= $\frac{1}{2}$ cung AB = $\frac{180}{2}$=90

=> tam giác CMD vuông tại M

Vì NMBD nội tiếp => \(\widehat{NDM}+\widehat{NBM}\) ( góc nội tiếp cùng chắn cung AM) 

Mà \(\widehat{MCD}+\widehat{NBM}\)=90

=> \(\widehat{MCD}+\widehat{NBM}\)=90 (1)

Mặt khác \(\widehat{NAB}+\widehat{NBA}\)=90 (2)

Từ (1) và (2) => \(\widehat{MCD}=\widehat{NAB}\)

Xét tam giác ANB và CMD ta cs

\(\widehat{ANB}=\widehat{CMD}\) (=90)

\(\widehat{MCD}=\widehat{NAD}\)

=> 2 tam giác này bằng nhau