trong mặt phẳng Oxy, viết phương trình chính tắc của elip có độ dài trục lớn bằng \(4\sqrt{2}\) đỉnh trên trục nhỏ và các tiêu điểm cùng nằm trên một đường tròn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 5 2017
a) \(\left(E\right):\dfrac{x^2}{100}+\dfrac{y^2}{36}=1\)
b) \(\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
Do 2 đỉnh trên trục nhỏ và 2 tiêu điểm tạo thành hình vuông \(\Rightarrow b=c\)
Mặt khác diện tích hình vuông bằng 32 \(\Rightarrow\dfrac{1}{2}.2b.2c=32\Rightarrow b^2=16\)
\(\Rightarrow a^2=b^2+c^2=2b^2=32\)
Phương trình: \(\dfrac{x^2}{32}+\dfrac{y^2}{16}=1\)
CM
4 tháng 11 2019
Ta có: độ dài trục nhỏ là 8 nên 2b = 8 => b= 4.
Độ dài tiêu cự là 10 nên 2c = 10 => c= 5.
Lại có : a2= b2+ c2= 16+ 25= 41
Vậy phương trình của Elip là: x 2 41 + y 2 16 = 1
Chọn D.
CM
23 tháng 4 2018
Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a 2 = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: a 2 - b 2 = c 2 ⇒ b 2 = a 2 - c 2 = 5 2 - 3 2 = 16
Vậy phương trình của elip (E) là:
CM
21 tháng 12 2017
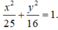
Ta có: độ dài trục lớn là 10 nên 2a= 10 => a= 5.
Độ dài tiêu cự là 6 nên 2c= 6 => c= 3
Ta có: b2 = a2- c2= 25- 9= 16 => b= 4
Vậy phương trình của Elip là: x 2 25 + y 2 16 = 1
Chọn A.
tại sao b=c vậy bạn?
Từ đề bài ta có: \(\left\{{}\begin{matrix}a=\frac{4\sqrt{2}}{2}=2\sqrt{2}\\b=c\end{matrix}\right.\)
\(\Rightarrow a^2=b^2+c^2=2b^2\)
\(\Rightarrow b^2=\frac{a^2}{2}=4\)
Phương trình elip: \(\frac{x^2}{8}+\frac{y^2}{4}=1\)