Mọi người giúp em giải câu này với :Chứng minh rằng (Tan2x/1+tan2x)(1+cot2x/cotx)=1+tan4x/tan2x+cot2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2019
\(\frac{2}{sin4x}-tan2x=\frac{2}{2sin2x.cos2x}-\frac{sin2x}{cos2x}=\frac{1}{cos2x}\left(\frac{1}{sin2x}-sin2x\right)\)
\(=\frac{1}{cos2x}\left(\frac{1-sin^22x}{sin2x}\right)=\frac{1}{cos2x}\frac{cos^22x}{sin2x}=\frac{cos2x}{sin2x}=cot2x\)
HP
25 tháng 6 2021
1. \(sin\left(\dfrac{\pi}{3}-x\right)\ne0\Leftrightarrow\dfrac{\pi}{3}-x\ne k\pi\Leftrightarrow x\ne\dfrac{\pi}{3}-k\pi\)
2. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
3. \(\sqrt{1+sinx}-\sqrt{2}\ge0\Leftrightarrow1+sinx\ge2\Leftrightarrow sinx\ge1\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
4. \(\sqrt{2-2cosx}-2\ne0\Leftrightarrow2-2cosx\ne4\Leftrightarrow cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
5. \(1-\sqrt{1+sin3x}\ne0\Leftrightarrow sin3x\ne0\Leftrightarrow3x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{3}\)
CM
14 tháng 10 2018
Chọn D
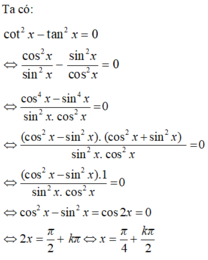
Vậy trong khoảng (0,2π), phương trình có các nghiệm là π 4 ; 3 π 4 ; 5 π 4 ; 7 π 4 nên tổng các nghiệm là 4π
27 tháng 6 2021
\(a,\tan10.\tan11......\)
\(=\left(\tan10.tan80\right)\left(tan11.tan79\right)....\left(tan44.tan46\right).tan45\)
Mà 10 và 80, 11 và 79, ... là các góc phụ nhau .
\(=tan10.cot10....tan45=1\)
b, Ta có : \(\tan x+\cot x=2\)
\(\Rightarrow\tan^2x+2\tan x\cot x+\cot^2x=4\)
\(\Rightarrow\tan^2x+\cot^2x=4-2=2\)
Ta có : \(\tan^3x+\cot^3x=\left(\tan x+\cot x\right)\left(\tan^2x-\tan x\cot x+\cot^2x\right)=2\)
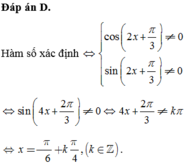
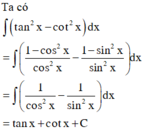
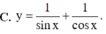
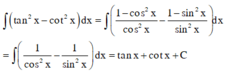
Đúng như bạn viết vế trái là thế này:
\(\left(\frac{tan^2x}{1+tan^2x}\right)\left(\frac{1+cot^2x}{cotx}\right)=\left(\frac{1}{\frac{1}{tan^2x}+1}\right)\left(\frac{1+cot^2x}{cotx}\right)\)
\(=\left(\frac{1}{cot^2x+1}\right)\left(\frac{1+cot^2x}{cotx}\right)=\frac{1}{cotx}=tanx\)
Còn vế phải sẽ ra thế này:
\(\frac{1+tan^4x}{tan^2x+cot^2x}=\frac{1+tan^4x}{tan^2x+\frac{1}{tan^2x}}=\frac{tan^2x\left(1+tan^4x\right)}{tan^4x+1}=tan^2x\)
Hai vế ra kết quả khác nhau nên chắc bạn ghi sai đề :)