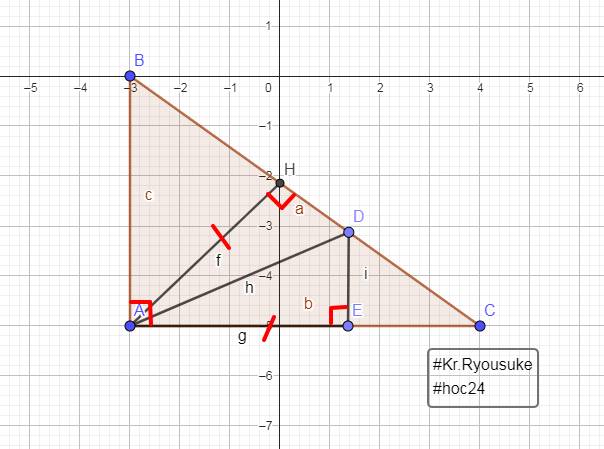
cho tam giác ABC vuông tại A, BC < AC,có đường cao AH. Lấy E thuộc AC sao cho AH = AE,qua E kẻ đường thảng vuông góc với AC cắt BC tại D, DE vuông góc AH tại K. M là trung điểm KC
cmr:
a) tam giác AHD = tam giác AED
b) so sánh DH và DC
c) Chứng minh A,D,M thẳng hàng