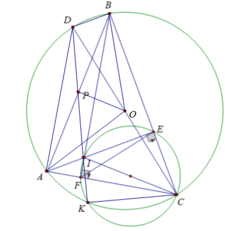
Câu 1: cho đường tròn (o) .hai đường cao BD,CE của tam giác ABC cắt nhau tại H. Đường tròn ngoại tiếp tam giác ADE cắt (o) tại điểm thứ hai K. Chứng minh rằng đường thẳng HK đi qua trung điểm M của BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 5 2022
Xin lỗi bạn nhưng máy mình bị lỗi không vẽ hình được.
c) Tứ giác BEDC là tứ giác nội tiếp (câu a) \(\Rightarrow\widehat{BDE}=\widehat{BCE}\) hay \(\Rightarrow\widehat{BDE}=\widehat{BCQ}\) (1)
Xét (O) có \(\widehat{BCQ}\) và \(\widehat{BPQ}\) là các góc nội tiếp chắn \(\stackrel\frown{BQ}\) \(\Rightarrow\widehat{BCQ}=\widehat{BPQ}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BDE}=\widehat{BPQ}\left(=\widehat{BCQ}\right)\)
\(\Rightarrow DE//PQ\) (2 góc đồng vị bằng nhau)
d) Kẻ tia tiếp tuyến Ax của (O) (ở đây mình lấy về phía B chứ còn bạn lấy tia tiếp tuyến này vế phía B hay phía C tùy)
Dễ thấy \(\widehat{BAx}\) và \(\widehat{ACB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\) \(\Rightarrow\widehat{BAx}=\widehat{ACB}\)
Tứ giác BEDC nội tiếp \(\Rightarrow\widehat{AED}=\widehat{ACB}\) (góc ngoài = góc trong đối)
\(\Rightarrow\widehat{BAx}=\widehat{AED}\left(=\widehat{ACB}\right)\) \(\Rightarrow Ax//DE\) ( 2 góc so le trong bằng nhau)
Vì \(DE//PQ\left(cmt\right)\) \(\Rightarrow Ax//PQ\)\(\left(//DE\right)\)
Mà \(Ax\perp OA\) tại A (do Ax là tiếp tuyến tại A của (O)) \(\Rightarrow OA\perp PQ\) (3)
Xét (O) có OA là 1 phần đường kính và \(OA\perp PQ\left(cmt\right)\)
\(\Rightarrow\) OA đi qua trung điểm của PQ (4)
Từ (3) và (4) \(\Rightarrow\) OA là trung trực của đoạn PQ
8 tháng 4 2021
1.
Chứng minh được .
Suy ra điểm cùng thuộc đường tròn đường kính nên tứ giác nội tiếp.
Có tứ giác nội tiếp nên ( góc nội tiếp cùng chắn cung ) hay .
Trong đường tròn tâm , ta có là góc nội tiếp chắn cung và nội tiếp chắn cung
.
2.
có nên hay .
Ta chứng minh được vừa là đường cao, vừa là phân giác của tam giác nên là trung điểm của .
Chứng minh tương tự là trung điểm của là đường trung bình của tam giác (1).
Do nên là điểm chính giữa cung (2).
Từ (1) và (2) suy ra .
3.
Kẻ đường kính của đường tròn tâm , chứng minh tứ giác nội tiếp đường tròn đường kính .
Chứng minh tứ giác là hình bình hành, suy ra .
Trong đường tròn có (2 góc nội tiếp cùng chắn cung ). Chỉ ra tam giác vuông tại và áp dụng hệ thức giữa cạnh và góc ta được cm.
Đường tròn ngoại tiếp tứ giác cũng là đường tròn ngoại tiếp tam giác .
Gọi là bán kính đường tròn ngoại tiếp tam giác .
Suy ra cm.
Vậy cm.
NN
22 tháng 8 2021
Do ^AEH=^ADH=90o nên tứ giác AEHD nội tiếp đường tròn.
Suy ra đường tròn ngoại tiếp tam giác AED chính là đường tròn đường kính AH.
Do H là giao điểm hai đường cao BD và CE nên H là trực tâm. Thế thì AH ⊥ BC.
Suy ra ^DAH=^DBC (vì cùng phụ với góc ^DCB).
Tam giác BDC vuông tại D có I là trung điểm của BC nên IB = ID = IC.
Suy ra tam giác IBD cân ở I. Vì vậy ^IDB=^DBI.
Từ đó suy ra: ^HAD=^HBI=^BDI hay ^HAD=^HDI.
Gọi J là trung điểm AH. Ta có ^HAD=^JDA⇒^JDA=^HDI.
Vậy nên ^JDI=^HDI+^JDH=^JDA+^FDH=^ADH=90o.
Suy ra DI là tiếp tuyến của đường tròn đường kính AH.
Chứng minh tương tự ta cũng có EI là tiếp tuyến của đường kính AH.
PV
22 tháng 8 2021
Do nên tứ giác AEHD nội tiếp đường tròn.
Suy ra đường tròn ngoại tiếp tam giác AED chính là đường tròn đường kính AH.
Do H là giao điểm hai đường cao BD và CE nên H là trực tâm. Thế thì AH BC.
Suy ra (vì cùng phụ với góc ).
Tam giác BDC vuông tại D có I là trung điểm của BC nên IB = ID = IC.
Suy ra tam giác IBD cân ở I. Vì vậy .
Từ đó suy ra: hay .
Gọi J là trung điểm AH. Ta có .
Vậy nên .
Suy ra DI là tiếp tuyến của đường tròn đường kính AH.
Chứng minh tương tự ta cũng có EI là tiếp tuyến của đường kính AH.
CM
11 tháng 2 2019
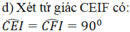
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.
