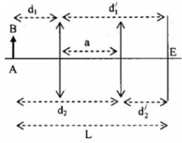
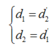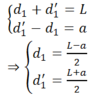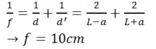Đặt vật sáng AB vuông góc với trục chính của 1 thấu kính hội tụ có tiêu cự f. Điểm A nằm trên trục chính cách thấu kính 1 khoảng d. Người ta thấy ảnh hứng được trên màn. Màn cách thấu kính 1 khoảng d' . Hãy chứng minh:
a) \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
b) \(\frac{1}{f}=\frac{1}{d}-\frac{1}{d'}\)
c) \(\frac{1}{f}=\frac{1}{d'}-\frac{1}{d}\)