Cho hình thang ABCD có AB song song với CD. Biết AB = 60cm, CD = 90cm, đường cao AH = 30cm. Trên cạnh AD lấy điểm E sao cho DE = 1/3 AD. Kẻ EF song song với DC. F nằm trên cạnh BC. Hãy so sánh EF và DC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vả lại tui cũng ddang gặp câu này mà bó tay.Các ae học giỏi giúp mị với

Kẻ đường chéo AC cắt EF tại I
Trong ΔADC, ta có: EI // CD
Suy ra: ![]()
Suy ra: 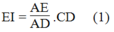
Lại có : 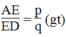
Suy ra: 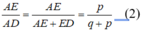
Từ (1) và (2) suy ra: ![]()
Trong ΔABC, ta có: FI // AB
Suy ra: ![]() (định lí ta-lét) (3)
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: ![]() (định lí ta-lét) (4)
(định lí ta-lét) (4)
Từ (3) và (4) suy ra 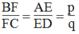
Trong ΔABC, ta có: IF // AB
Suy ra: 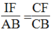 (định lí ta-lét)
(định lí ta-lét)
Suy ra: ![]()
Ta có: 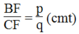
Suy ra: 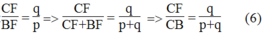
Từ (5) và (6) suy ra: ![]()
Vậy: 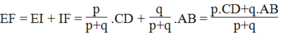

Hình thang ABCD (AB//CD) có: M là trung điểm AE, MN//AB//EF.
\(\Rightarrow\)N là trung điểm BF nên MN là đường trung bình của hình thang ABCD.
\(\Rightarrow MN=\dfrac{AB+EF}{2}=\dfrac{12+18}{2}=15\left(cm\right)\).
Hình thang MNCD (MN//CD) có: E là trung điểm MD, EF//MN//CD.
\(\Rightarrow\)F là trung điểm CD nên EF là đường trung bình của hình thang MNCD.
\(\Rightarrow EF=\dfrac{MN+CD}{2}\Rightarrow CD=2EF-MN=2.18-15=21\left(cm\right)\)

Gọi I là giao của EF và BD.
Vì EF//AB, áp dụng ta-lét vào tam giác DAB,ta có:\(\frac{EI}{AB}=\frac{ED}{DA}=\frac{5}{17.5}=\frac{DI}{BD}\)(1)
Vì IF//DC ,áp dụng Ta-lét vào tam giác BDC,ta có :\(\frac{DC}{IF}=\frac{DB}{IB}\)(2)
Từ (1),(2) \(\Rightarrow\)\(\frac{DI}{DB}.\frac{DB}{IB}=\frac{DI}{IB}=\frac{5}{12.5}\)
\(\Rightarrow\)\(\frac{DC}{IF}.\frac{5}{17.5}=\frac{5}{12.5}\Rightarrow\frac{IF}{DC}=\frac{12.5}{17.5}\)
Mà DC=35\(\Rightarrow\)IF =\(\frac{12.5}{17.5}\)\(\times\)35=25.
Từ (1)vì AB=14\(\Rightarrow\)EI=\(\frac{5}{17.5}\times14\)=4
Vậy IF+IE=25+4=29.

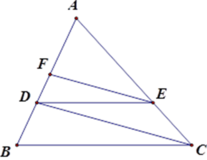
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C
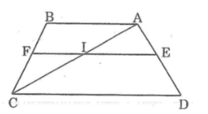
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD