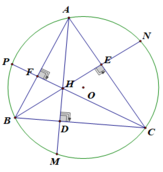
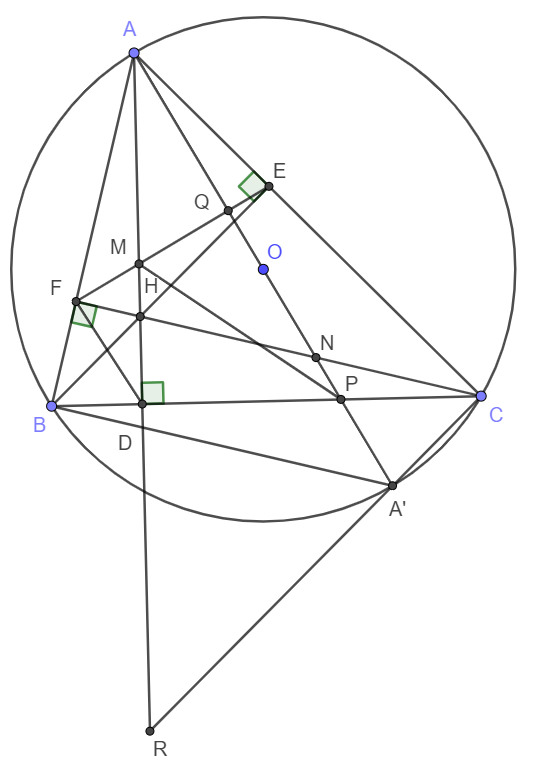
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD và BE cắt nhau tại H nằm trong tam giác ABC. Gọi M, N lần lượt là giao điểm của AD và BE với đường tròn (O).
a) CMR: 4 điểm A, E, D, B cùng thuộc 1 đường tròn
b) MN\(\)// DE
c) CO vuông góc với DE
d) Cho AB cố định. Xác định C trên cung lớn AB để diện tích tam giác ABC lớn nhất