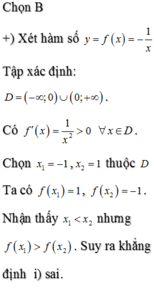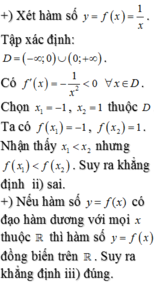cho hàm số y=f(x) xác định với mọi x thuộc Q thỏa mãn với mọi x1,x2 thuộc Q thì f(x1+x2) và f(100) =2020. Tính f(-100)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
0
17 tháng 2 2020
Theo c) \(f\left(\frac{5}{7}\right)=f\left(\frac{2}{7}+\frac{3}{7}\right)=f\left(\frac{2}{7}\right)+f\left(\frac{3}{7}\right)\)
\(f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}+\frac{1}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{1}{7}\right)=2.f\left(\frac{1}{7}\right)\)
\(f\left(\frac{3}{7}\right)=f\left(\frac{1}{7}+\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+2f\left(\frac{1}{7}\right)=3.f\left(\frac{1}{7}\right)\)
\(\implies\)\(f\left(\frac{5}{7}\right)=5.f\left(\frac{1}{7}\right)\) (1)
Theo b) \(f\left(\frac{1}{7}\right)=\frac{1}{7^2}.f\left(7\right)\) (2)
Theo c) \(f\left(7\right)=f\left(3+4\right)=f\left(3\right)+f\left(4\right)\)
\(=2.f\left(3\right)+f\left(1\right)\)
\(=6.f\left(1\right)+f\left(1\right)\)
\(=7.f\left(1\right)\)
Theo a)\(f\left(1\right)=1\)\(\implies\)\(f\left(7\right)=7\) (3)
Từ (1);(2);(3)
\(\implies\) \(f\left(\frac{5}{7}\right)=\frac{5}{7}\)
NT
0
26 tháng 12 2018
Giải:
Vì f(x1x2)=f(x1).f(x2) nên ta có:
f(4)=f(2.2)=f(2).f(2)=5.5=25
Mà:
f(2)=5
⇔f(8)=f(4.2)=f(4).f(2)=25.5=125
Vậy: f(8)=125
4 tháng 1 2021
\(f\left(243\right)=f\left(3\cdot81\right)=-2\cdot f\left(3\cdot27\right)=4\cdot f\left(3\cdot9\right)=-8\cdot f\left(3\cdot3\right)=16\cdot\left(-2\right)=-32\)
