Tìm các số nguyên tố p sao cho 7p+1 là lập phương của một số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
5
2 tháng 9 2018
Lý thuyết :
Số nguyên tố là số tự nhiên lớn hơn 1 và chỉ có 2 ước là 1 và chính nó. Mọi số tự nhiên >1 bao giờ cũng có ước nguyên tố .
- Hợp số là số tự nhiên lớn hơn 1 và có nhiều hơn 2 ước
- Tập hợp số nguyên tố là vô hạn
- Số 0 và 1 không phải là số nguyên tố; cũng không là hợp số
- Số nguyên tố chẵn duy nhất là 2
- Số a và b gọi là 2 số nguyên tố cùng nhau
- p là số nguyên tố; p > 2 có dạng : p = 4n + 1 hoặc p= 4n+3
- p là số nguyên tố; p > 3 có dạng : p = 6n +1 hoặc p =6n + 5
- Ước nguyên tố nhỏ nhất của hợp số N là 1 số không vượt quá √N
- số nguyên tố Mecxen có dạng 2^p - 1 (p là số nguyên tố )
- Số nguyên tố Fecma có dạng 2^(2n) + 1 (n Є N)
Khi n = 5. Euler chỉ ra 2^(2.5) + 1 = 641.6700417 (hợp số )
Bài tập:
Đặt 2p + 1 = n³ với n là số tự nhiên
Cách giải: phân tích ra thừa số
Dùng tính chất : Số nguyên tố có 2 ước là 1 và chính nó.
Giải:
♣ Ta thấy p = 2 thì 2p + 1 = 5 không thỏa = n³
♣ Nếu p > 2 => p lẻ (Do Số nguyên tố chẵn duy nhất là 2 )
Mặt khác : 2p + 1 là 1 số lẻ => n³ là một số lẻ => n là một số lẻ
=> 2p + 1 = (2k + 1)³ ( với n = 2k + 1 )
<=> 2p + 1 = 8k³ + 12k² + 6k + 1
<=> p = k(4k² + 6k + 3)
=> p chia hết cho k
=> k là ước số của số nguyên tố p.
Do p là số nguyên tố nên k = 1 hoặc k = p
♫ Khi k = 1
=> p = (4.1² + 6.1 + 3) = 13 (nhận)
♫ Khi k = p
=> (4k² + 6k + 3) = (4p² + 6p + 3) = 1
Do p > 2 => (4p² + 6p + 3) > 2 > 1
=> không có giá trị p nào thỏa.
Đáp số : p = 13
thay 2p+1 là 7p+1 nha
thay vào mak tự làm sẽ thông minh hơn@@
DB
2 tháng 9 2018
\(7p+1=a^3\)( a là số nguyên )
\(\Rightarrow7p=a^3-1\)
\(\Rightarrow7p=\left(a-1\right)\left(a^3+a+1\right)\)( Phân tích ra hằng đẳng thức )
\(\Rightarrow7p⋮a-1\)
Mà 7 và p đều là các số nguyên tố nên ta xét 2 trường hợp:
Làm nốt đi xét các trường hợp rồi thay vô giải là xong nha :3
NV
5
VT
2 tháng 3 2018
Đặt \(7P+1=a^3\Rightarrow7P=\left(a-1\right)\left(a^2+a+1\right)\)
vì P là số nguyên tố => 7P là tích 2 số nguyên tố
=>\(\left(a-1\right)\left(a^2+a+1\right)\) là tích 2 số nguyên tố
nếu 1 trong 2 biểu thức a-1 hoặca^2+a+1 là hợp số => số còn lại =1
xét a^2+a+1 là hợp số => a-1=1 => a=2, thay vào tìm P
xét a-1 là hợp số => a^2+a=1=1 => a=0 hoặc a=-1, thay vào tìm P
nếu cả 2 số là số nguyên tố , ta cx xét 2 TH
TH1: a-1=7
TH2: a^2+a+1=7
=> ....
Tôi nghĩ vậy, nếu sai thì thôi :V
2 tháng 3 2018
Hợp số là một số tự nhiên có thể biểu diễn thành tích của hai số tự nhiên khác nhỏ hơn nó. Một định nghĩa khác tương đương: hợp số là số chia hết cho các số khác ngoài 1 và chính nó.[1][2]
Mọi số nguyên dương bất kỳ hoặc là 1, hoặc là số nguyên tố, hoặc là hợp số.
Định lý cơ bản của số học nói rằng mọi hợp số đều phân tích được dưới dạng tích các số nguyên tố và cách biểu diễn đó là duy nhất nếu không tính đến thứ tự của các thừa số.[3][4][5][6][7].
- Mọi số chẵn lớn hơn 2 đều là hợp số.
- Mọi hợp số không phải là số nguyên tố.
- Hợp số nhỏ nhất là 4.
NN
1
14 tháng 2 2021
Đặt \(13p+1=n^3\left(n\in N\right)\)
\(\Leftrightarrow13p=n^3-1\)
\(\Leftrightarrow13p=\left(n-1\right)\left(n^2+n+1\right)\)
Trường hợp 1: \(n-1=13\forall n^2+n+1=p\)
\(\Leftrightarrow n=14\)
hay \(p=14^2+14+1=196+14+1=211\)(nhận)
Trường hợp 2: \(n-1=p\forall n^2+n+1=p\)
\(\Leftrightarrow n^2+2=13-p\)
\(\Leftrightarrow\left(p+1\right)^2=11-p\)
\(\Leftrightarrow p=2\)(nhận)
Vậy: \(p\in\left\{2;211\right\}\)
CM
15 tháng 7 2017
1.Với a = 2 ta có 2a + 1 = 5 không thích hợp
Với a ≠ 2 do a là số nguyên tố nên a lẽ
Vậy 2a + 1 là lập phương của một số lẽ nghĩa là
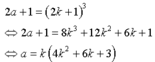
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a
-Nếu k = 1 thì 2a + 1 = (2.1 + 1)3 suy ra a = 13 thớch hợp
- Nếu a = k từ a = a(4a2 + 6a + 3) do a là nguyên tố nên suy ra
1 = 4a2 + 6a + 3 không có số nguyên tố a nào thoả món phương trỡnh này Vì vế phải luụn lớn hơn 1
Vậy a = 13
2.Giả sử
13 và p là các số nguyên tố , mà n – 1 > 1 và n2 + n + 1 > 1
Nên n – 1 = 13 hoặc n – 1 = p
- Với n – 1 =13 thì n = 14 khi đó 13p = n3 – 1 = 2743 suy ta p = 211 là số nguyên tố
- Với n – 1 = p thi n2 + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố
Vậy p = 2, p = 211 thì 13p + 1 là lập phương của một số tự nhiên
4 tháng 2 2020
Đặt 7p+1=n3(n>2)(n\(\inℕ\))
=>7p=(n-1)n(n+1)=(n-1)(n2+n+1) *
Xét p=2=>loại
Xét p>2=>p là số nguyên tố lẻ
Mà n2+n+1=n(n+1)+1 luôn lẻ
Từ * ta có \(\hept{\begin{cases}n-1=7\\n^2+n+1=p\end{cases}}\Leftrightarrow\hept{\begin{cases}n=8\\p=31\end{cases}}\)
(THOẢ MÃN)
4 tháng 9 2016
xin lỗi tớ nhầm
Đặt 2p + 1 = n³ với n là số tự nhiên
Cách giải: phân tích ra thừa số
Dùng tính chất : Số nguyên tố có 2 ước là 1 và chính nó.
Giải:
♣ Ta thấy p = 2 thì 2p + 1 = 5 không thỏa = n³
♣ Nếu p > 2 => p lẻ (Do Số nguyên tố chẵn duy nhất là 2 )
Mặt khác : 2p + 1 là 1 số lẻ => n³ là một số lẻ => n là một số lẻ
=> 2p + 1 = (2k + 1)³ ( với n = 2k + 1 )
<=> 2p + 1 = 8k³ + 12k² + 6k + 1
<=> p = k(4k² + 6k + 3)
=> p chia hết cho k
=> k là ước số của số nguyên tố p.
Do p là số nguyên tố nên k = 1 hoặc k = p
♫ Khi k = 1
=> p = (4.1² + 6.1 + 3) = 13 (nhận)
♫ Khi k = p
=> (4k² + 6k + 3) = (4p² + 6p + 3) = 1
Do p > 2 => (4p² + 6p + 3) > 2 > 1
=> không có giá trị p nào thỏa.
Đáp số : p = 13
Đặt 7p + 1 = n^3 (n > 2)
=> 7p = (n - 1)(n^2 + n + 1)
Ta có 2 TH :
TH1 : n - 1 = 7 \(\forall\)n^2 + n +1 = p => n = 8 => p = 73
TH2 : n - 1 = p \(\forall\) n^2 + n + 1 =7 => ....