Tính diện tích hình thoi ABCD có hai đường chéo AC = 6 cm, BD = 8 cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LU
19 tháng 1 2018
mình có ac gấp 3 lần đg chéo bd nên ac = 3bd
ac dài hơn bd 8cm -> ac - bd = 8 (1)
<=> 3bd -bd = 8
<=> 2bd = 8
<=> bd = 4cm
Thay bd vào biểu thức (1), có: ac - 4 = 8
=> ac =12cm
BB
1
20 tháng 9 2021
Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)
⇒O là trung điểm của AC và BD
⇒AO=AC2 và DO=BD2
=> AO=6/2=3(cm) và DO = 8/2= 4cm
AC vuông góc BD TẠI O ( vì ABCD là hình thoi )
tam giác ADO vuông góc tại O có AD bình = AO bình + DO bình ( định lý pytago)
=> AD2 =3 bình + 4 bình = 25 => AD= 5cm
Vậy AB=BC=DC=AD=5cm
CM
5 tháng 11 2019
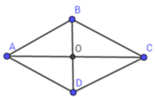
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
CM
9 tháng 5 2017
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
Giải
Diện tích hình thoi ABCD là:
\(S_{ABCD}=\frac{1}{2}.AB.BD=\frac{1}{2}.6.8=24\left(cm^2\right)\)
Vậy \(S_{ABCD}=24cm^2\)
#hình hơi xấu=)#
#hoktot<3#