Gọi \(x_1;x_2;x_3;x_4\) là các nghiệm của phương trình: \(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)=1\)
Tính \(x_1\cdot x_2\cdot x_3\cdot x_4\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
-1/7 . 7/3 ; -4 ; -43/10
=-7/3 ; -4 ; -43/10
nhớ tính lại từ đây nha=-7/3 ; -4/1 ; -43/10
= -7/3 . -1/4 ; -43 /10
= 8/12; -43/10
=8/12 . -10/43
= -80/516
CM
7 tháng 2 2019
Chọn C
Điều kiện
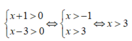
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
\(\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)-1=0\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)-1=0\)
Đặt \(x^2+8x+7=t\) (1)
\(t\left(t+8\right)-1=0\)
\(\Leftrightarrow t^2+8t-1=0\)
Do \(ac< 0\) nên pt luôn có 2 nghiệm pb: \(\left\{{}\begin{matrix}t_1+t_2=8\\t_1t_2=-1\end{matrix}\right.\)
- Với nghiệm \(t_1\) thay vào (1) ta có:
\(x^2+8x+7-t_1=0\)
Theo Viet, pt này có 2 nghiệm thỏa: \(x_1x_2=7-t_1\)
Với nghiệm \(t_2\) ta có: \(x^2+8x+7-t_2=0\)
Pt này có 2 nghiệm thỏa Viet: \(x_3x_4=7-t_2\)
Do đó: \(x_1x_2x_3x_4=\left(7-t_1\right)\left(7-t_2\right)\)
\(=49-7\left(t_1+t_2\right)+t_1t_2=49-7.8-1=-8\)
\(t_1+t_2=-8\)